Functions and Rates of Change (Business)

What is a Function?

A function is like a machine that takes a number (an input), changes this number (by adding another number to it, multiplying it by another number etc.) and gives back the changed number (an output). The output is always related to the input in some way so the same input will always give the same output. This output is unique, which means that each output can only be produced from a single input.

Call the input $x$ and the output $f$. The output corresponding to the input $x$ is denoted by $f(x)$. For instance, the function $f(x) = x^2 + 4$ says that for each value of $x$ the function $f$ squares it and adds 4. For $x=3$, we have \begin{align} f(3) &= 3^2 + 4\\ &=9+4\\ &=13. \end{align}

For more information on functions see Functions.

Example

Suppose that a company manufactures luxury sports cars and is interested in the total production cost of its cars. The cost of production $C$ (in $£$) depends on (is a function of) the quantity of cars produced $Q$. The cost function for this company’s cars is given by: \[C= 30Q^2 - 150Q + 2,000.\]

This is a function because given any value of $Q$ the formula gives a corresponding value of $C$. This means that by substituting different values of $Q$ into this equation we can determine the total costs of producing $Q$ cars.

Suppose the company chooses to produce $10$ cars. Then the total cost of production is: \[C= 30\times100 - 150\times10 + 2,000 = 3,500\]

So the total cost of producing $10$ cars is $£3,500$.

A graph of a function is a useful way of visualising what the function does. For instance, the plot below shows the graph of $C(Q)=30Q^2-150Q+1,000$ from $Q=0$ to $Q=4,000$.

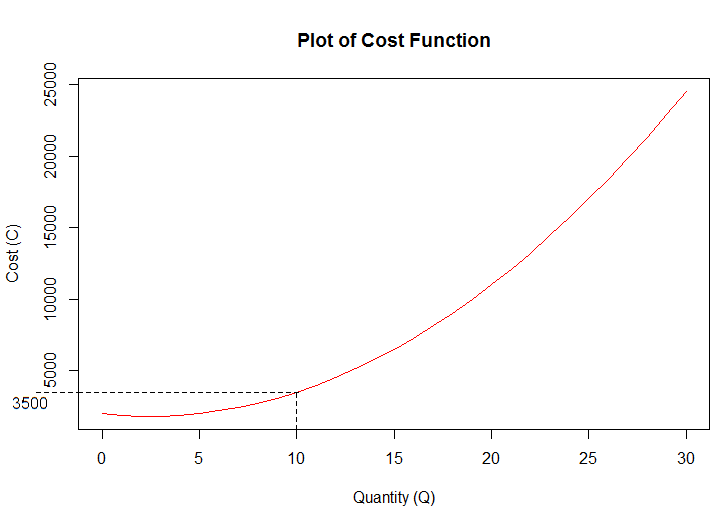
We can see that for every point on the graph, the value of $Q$ at that point corresponds to a unique value of $C$.

The Derivative

We are often interested in the rate of change or slope of a function $f(x)$ in terms of the input variable $x$. This is known as the derivative of the function $f(x)$ with respect to $x$ and is denoted by \[\dfrac{\mathrm{d}f}{\mathrm{d}x}\]

or $\dfrac{\mathrm{d}y}{\mathrm{d}x}$ if we denote the output of the function by $y=y(x)$.

Alternative notations for the derivative $\dfrac{\mathrm{d}f}{\mathrm{d}x}$ include

• $\dfrac{\mathrm{d}(f(x))}{\mathrm{d}x}$, and
• $f’(x).$

The table below gives a list of standard derivatives which you should be familiar with and be able to use:

$f(x)$	$\dfrac{\mathrm{d}f}{\mathrm{d}x}$
$x^n$	$nx^{n-1}$
$kx$	$k$
$\ln{x}$	$\frac{1}{x}$
$\mathrm{e}^{x}$	$\mathrm{e}^{x}$
$a^x$	$a^x\ln{a}$
$\sin{x}$	$\cos{x}$
$\cos{x}$	$-\sin{x}$
$\tan{x}$	$\sec^2{x}$

Have a look at the following resources if you need a reminder on derivatives and how to calculate them:

• Basic differentiation - a refresher workbook at mathcentre.
• Table of derivatives leaflet at mathcentre.
• Extending the table of derivatives workbook at mathcentre.
• Facts and Formulae leaflet from mathcentre has a table of derivatives and the rules for differentiation.
• Taking derivatives at Khan Academy

Applications of Rates of Change

Marginal Revenue

Marginal revenue is the additional revenue generated by increasing the quantity of a product sold by one unit. In other words, it is the rate of change, or derivative, of the total revenue function $R=PQ$ with respect to quantity sold $Q$:

\[MR=\dfrac{dR}{dQ}\].

Another way of thinking about marginal revenue is that it is the ratio of a change in revenue $\triangle R$ to the corresponding change in demand or quantity sold $\triangle Q$.

\[MR=\dfrac{\triangle R}{\triangle Q}\].

Note: In some cases we can also express $Q$ and $R$ as marginal functions in terms of other variables. For instance $Q$ could be a function of workforce hours $H$, so $Q = f(H)$. Then the marginal product of worked hours would be $\dfrac{dQ}{dH}$. This tells us how much more is produced for an additional hour of work.

Worked Example 1

Price Elasticity and Demand Functions

There are many types of demand function. One important such function is the price elasticity of demand E which is a measure of how sensitive demand for a product is to a small change in the price. In other words, it is the percentage change in quantity demanded caused by a one percent change in price of the good. The formula for E is:

If the price elasticity of demand is less than one $(E \lt 1)$, then we say demand is inelastic, which means it is insensitive to price changes, so if the price of a product changes (increased or decreased) the demand for the good would not change much (for example fuel). If the price elasticity of demand is greater than one demand is elastic $(E \gt 1)$, meaning it is sensitive to price changes, so if the price changes then the demand for the good will change a lot (for example luxury food items).

Recasting this into mathematics

In order to use some of the mathematics and the demand functions we have developed earlier it is useful to derive $E$ in terms of $Q$ and $P$ as follows.

From the percentage section in Background mathematics we can represent this formula mathematically as:

This equation gives us the average sensitivity of demand for a set of prices $P_1$ to $P_2$. To find the price elasticity of demand at a particular point $(P_i,Q_i)$ which is extremely close to the point $(P, Q)$ instead of calculating $\triangle P$ and $\triangle Q$ we find the differential $\dfrac{dQ}{dP}$ instead. So the formula for the price elasticity of demand at $P$ is:

Worked Example 2