Numeracy, Maths and Statistics - Academic Skills Kit

Decision Making Using Probability (Business)

ContentsToggle Main Menu 1 Expected Monetary Value 2 Tree Diagrams 3 Worked Example 1 4 Decision Trees 5 Worked Example 2 6 Test Yourself 7 See Also

Expected Monetary Value

The Expected Monetary Value $(\mathrm{EMV})$ of a single event is calculated as the sum of the monetary value of each outcome in that event multiplied by its probability. That is,

\begin{equation} \mathrm{EMV} = \sum{\mathrm{P}(\text{Event})} \times \text{Monetary Value of Event} \end{equation}

where the sum is over all possible outcomes in the event.

Tree Diagrams

Tree Diagrams can be used to help us to visualise and calculate complex probabilities. When drawing a tree diagram we begin with a dot. From this dot lines (“branches”) are then drawn, extending from the right of the first dot, to represent all possible outcomes for the given situation. The probabilities of each of these outcomes is written just above the corresponding line.

To calculate the probability that two events both happen, we draw another “branch” extending from the “branch” corresponding to one of these events to represent the second event occurring after the first. Above this line we write the probability (or conditional probability for events which are not independent) of the second event occurring after the first. Multiplying these probabilities “along the branches” gives the required probability.

To calculate the probability that one or both of two independent events occurs we add the probabilities of the two events “down the columns”.

The following example illustrates this idea:

Worked Example 1

Worked Example

$60\%$ of employees at a department store in Newcastle are women. Government research into methods of commuting to city jobs in the North East has shown on average that:$ \;$

$12\%$ of people cycle into work.
A quarter of the people drive.
$10\%$ of people walk.
And the rest use public transport.

What is the probability that a randomly selected employee is female and drives into work.

Solution

We can use a tree diagram to present all of the information given to us and calculate the required probability.

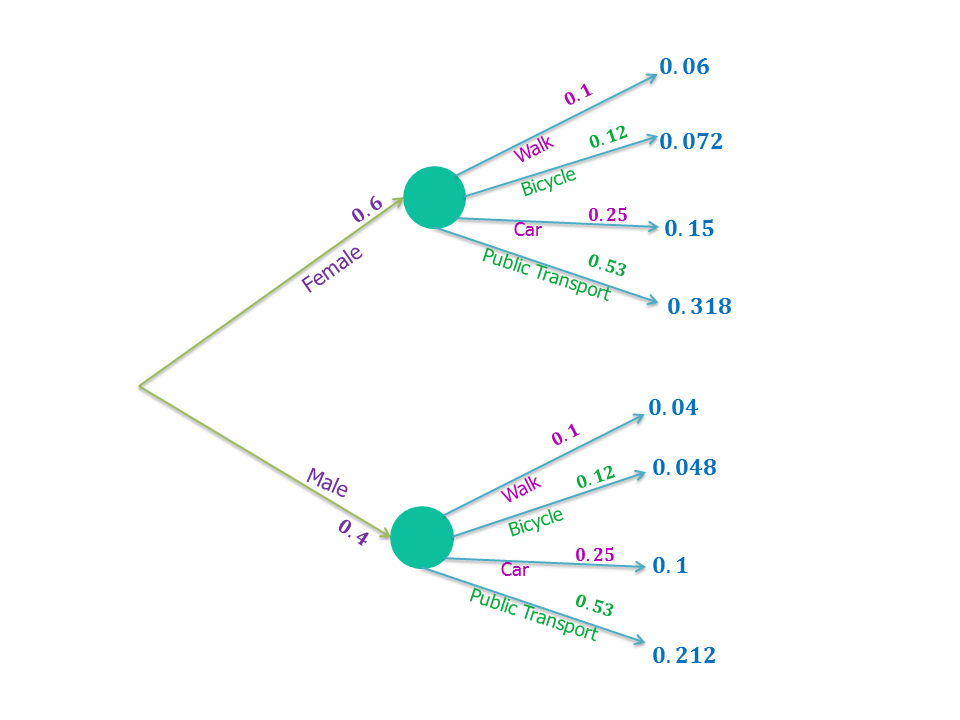
|center

The probabilities in blue are calculated using the multiplication law. So, the probability the employee is female and drives is $0.6 \times 0.25 = 0.15$.

Tip: To make sure all your calculations are correct, you can check to see that your final probabilities (the blues ones) add up to $1$. This must be the case because at least one of all of the possible events must (is certain to) occur.

Decision Trees

Decision trees are very similar to the probability tree diagrams but are used specifically to calculate expected monetary values.

Worked Example 2

Worked Example

The manager of a small business has the opportunity to buy a fixed quantity of a new product and offer it for sale for a limited time.

There will be a fixed cost of $£100,000$ to buy the product and offer it for sale. The amount of the product that the manager would be able to sell is not certain but market research has suggested that:

The probability that sales would be “poor” is $0.25$. Selling this quantity would raise an income of $£75,000$.
The probability that sales would be “medium” is $0.6$. Selling this quantity would raise an income of $£110,000$.

The probability that sales would be “good” is $0.15$. Selling this quantity would raise an income of $£145,000$.

The product can be sold for a trial period before a final decision is made and it costs $£18,000$ to run the trial. The results of the trial will be “poor” with probability $0.35$, “medium” with probability $0.4$ or “good” with probability $0.25$. Knowing the outcome of the trial changes the probabilities for the main sales project:

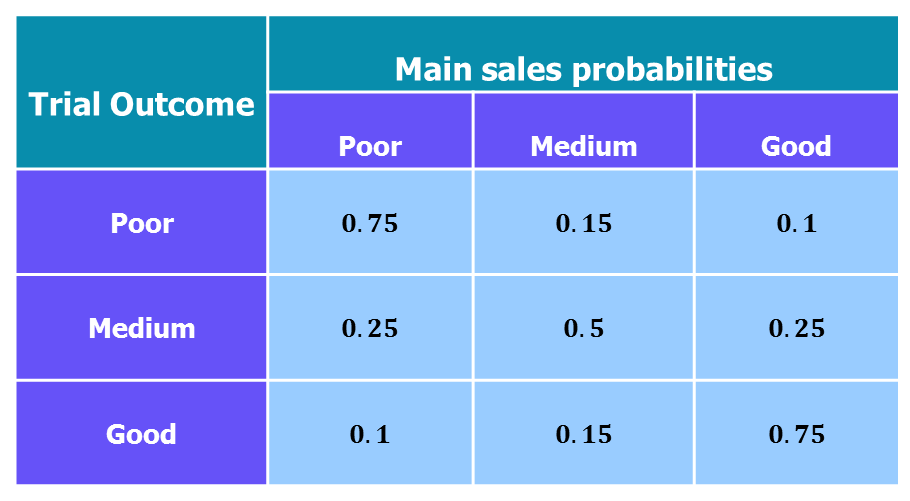
The manager will make decisions based on expected monetary value.

(A) Draw a decision tree for this problem.

(B) What is the $\mathrm{EMV}$ of a decision to go ahead with the product without a trial?

(C) Complete the solution of the decision problem and determine the optimal course of action for the company.

Solution

A) |center

The values in the blue boxes are the final incomes from buying the new product when sales are “poor”, “medium” or “good” (top to bottom).

B) To calculate the expected monetary value we need to utilise the formula in the pink box above.

For No Trial:

\begin{align} \mathrm{EMV} &= 0.25 \times £75,000 + 0.6 \times £110,000 + 0.15 \times £145,000\\ &=£106,500.\\ \end{align}

The manager has an expected income of $£106,500$ from selling the new product without a trial.

C) To solve the decision problem it is best to first calculate the seperate $\mathrm{EMV}$s for when a trial is run and when a trial is not run. We must then compare the $\mathrm{EMV}$s for each option (trial or no trial) and choose the option with the highest $\mathrm{EMV}$. This is the optimal course of action for the company.

When a trial is carried out and has a poor result:

\begin{align} \mathrm{EMV} &= 0.75 \times £75,000 + 0.15 \times £110,000 + 0.1 \times £145,000\\ &=£87,250.\\ \end{align}

When a trial is carried out and has a medium result:

\begin{align} \mathrm{EMV} &= 0.25 \times £75,000 + 0.5 \times £110,000 + 0.25 \times £145,000\\ &=£110,000.\\ \end{align}

When a trial is carried out and has a good result:

\begin{align} \mathrm{EMV} &= 0.1 \times £75,000 + 0.15 \times £110,000 + 0.75 \times £145,000\\ &=£132,750.\\ \end{align}

Now to calculate the overall $\mathrm{EMV}$ we multiply each of these by their associated probabilities: \begin{align} \mathrm{EMV} &= \mathrm{P}(\text{Poor result}) \times £87,250 + \mathrm{P}(\text{Medium result)} \times £110,000 \\ &\;\;\;\;+ \mathrm{P}(\text{Good result}) \times £132,750\\ &=£107,725. \end{align}

We now need to calculate the expected profit (or loss) the business would make from each option (trial or no trial).

No Trial:

\begin{align} \text{Expected Profit} &= \mathrm{EMV} \text{ for no trial} - \text{Cost of new product}\\ &=£106,500 - £100,000\\ &=£6,500. \end{align}

So if the manager goes ahead with the product without a trial, the expected profit is $£6,500$.

Trial:

\begin{align} \text{Expected Profit} &= \mathrm{EMV}\text{ for trial} - \text{Cost of new product} - \text{Cost of trial}\\ &=£107,725 - £100,000 - £18,000\\ &=-£10,275. \end{align}

With the trial, there will be an expected loss of £10,275.

From these results we can see that optimal course of action for the company is to sell the new product but without the trial period as this yields a higher $\mathrm{EMV}$. It is important to note that although the expected monetary value is higher when the manager chooses not to run the trial, the realised profit or loss may be or may not be better than it would have been if a trial had been carried out.

Test Yourself

Test yourself: Probability