Numeracy, Maths and Statistics - Academic Skills Kit

Descriptive Statistics (Business)

ContentsToggle Main Menu 1 Descriptive Statistics 2 Sampling 3 Descriptive Statistics: Measures of Location 4 Measures of Spread 5 Data Types 6 Summary Statistics 7 Test Yourself 8 See Also

Descriptive Statistics

Given a dataset your task may be to try to describe the main features of the data. For example, you may want to know dispersed the data are about a central value. This will give you an idea of the variability of the dataset. Descriptive statistics provide summaries of the main features of a dataset.

If all the dataset information is available to you and you have sufficient software to analyse it e.g. R, SPSS or Minitab, then your task is to put the information into the program and analyse it appropriately. However, the dataset information you want may not be fully available to you. This is particularly true for large populations where it is not feasible to extract all the data , e.g. for the the UK population; voting preferences, number of cars per household etc.. In this case the usual method is to sample the population and analyse the sample.

Sampling

We take the relevant information from a small, but adequate for our purpose, percentage of of the actual population to draw conclusions and test hypotheses. For example, if we wanted to test, How many hours do teachers in the state sector work in an average week in the UK? it would not be feasible to find this information from every such teacher. Therefore we take an appropriate sample of the population and make reasonable assumptions about the overall population from our sample data.

For more information on this see sampling.

Descriptive Statistics: Measures of Location

The Arithmetic Mean: This is calculated by summing the data values you have and dividing by the number of data items. For example, you could use the mean to calculate the average number of telephone sales per day of your employees.
Sample Mean: If you have a sample of data consisting of $n$ observations $(x_1,...,x_n)$ then the mean $(\bar{x})$ of this sample is calculated using the formula:

\begin{equation} \bar {x} = \frac{1}{n}\sum\limits_{i=1}^{n}\ x_i. \end{equation}

The Population Mean: The population mean, denoted by $\mu$, is the mean for the entire population. If you do not know the population mean, then we can take a random sample of sufficient size, find its mean and then there are various methods which allow us to estimate the population mean from this. For example, we might take a sample of GCSE business scores instead of collecting all of the GCSE business scores from everyone in the country.

The Mode: The mode is the most frequently occurring value in the data set. For instance the modal value of the dataset: $3,4,4,5,4,6,7,8$ is $4$ as $4$ occurs twice whereas the other values each occur only once. For example, we might want be interested in which of a company's products is most popular.

The Median: The median can be viewed as the middle value of the dataset. To calculate this value, order the data values by increasing size, then:

For an odd number of data points the median is the value that is in the middle. For example in the ordered set $1,3,3,3,4,6,7,7,8$ the median is the fifth number in this set which is $4$.

If you have an even number of observations then there is no one middle number so you must average the middle two values i.e. $\big(\frac{n}{2}\big)^\text{th}$ and $\big( \frac{n}{2} +1\big)^\text{th}$ values. For example in the ordered set $10,13,14,14,16,17,17,17,18,19$, the median is the average of the middle two numbers; the fifth, $16$ and the sixth, $17$. Hence the median is $16.5$

See Mean, median and mode and Weighted averages for more information and more complex examples.

Measures of Spread

The Range: The range measures the difference between the size of the largest value in the data set and the smallest. For instance we could use the range for market research - to find out the range of income of your clients. We calculate the range using the formula:

\begin{equation} \text{Range} =\text{Largest value}- \text{ smallest value}. \end{equation}

The Sample Variance : Given a sample from the population you are studying, the sample variance is the measurement of the squared distances of the data values from the mean of the sample. The variance is calculated by the formula:

\begin{equation} s^2 = \frac{1}{n-1}\sum\limits_{i=1}^n(x_i - \bar {x})^2. \end{equation}

The Sample Standard deviation: The sample standard deviation is the positive square root of the sample variance. Like the sample variance, it is a measure of much the sample data deviates from the mean of the sample and is usually denoted by $s$. The sample standard deviation could be used to monitor how much the daily sales of a product in a store fluctuates - big standard deviations could mean some days with really low or high total sales. It is calculated using the formula:

\begin{equation} s = \sqrt{\frac{1}{n-1}\sum\limits_{i=1}^n(x_i - \bar {x})^2}. \end{equation}

'' The Population Variance'' : The population variance is very similar to the sample variance however this measures the actual spread of the whole population. The only difference in the calculation is that instead of dividing by $n-1$ we divide by the number of data points in the population,$n$, so the formula becomes:

\begin{equation} \sigma^2 = \frac{1}{n}\sum\limits_{i=1}^n(x_i - \bar {x})^2. \end{equation}

The Population Standard Deviation: The population standard deviation (SD) is the positive square root of the population variance.

\begin{equation} \sigma = \sqrt{\frac{1}{n}\sum\limits_{i=1}^n(x_i - \bar {x})^2}. \end{equation}

'' The Interquartile range (IQR) '' : The IQR measures the range of the middle half of the data, and so is less affected by extreme observations. It is given by $Q3 - Q1$, where:

\begin{equation} \begin{split} &&Q1 = \frac{(n+1)}{4}^\text{th} \text{ smallest observation} \\&& Q3 = \frac{3(n+1)}{4}^\text{th} \text {smallest observation}. \end{split} \end{equation}

The Standard Error (SE) of the Mean: Given a sample taken from a population, the sample mean is an estimator of the population mean. The standard error of the mean is a measure of the spread of the error caused by using the sample mean to estimate the population mean. We calculate it using the following formula:

\begin{equation} \text{Standard Error (SE)} = \frac{s}{\sqrt{n}}. \end{equation}

For more information see Variance and standard deviation

Notation in the above formulas explained:

\begin{equation} \begin{split} &&\bar{x} = \text{Arithmetic mean} \\ &&x = \text {Individual data value} \\ &&s = \text{ Sample standard deviation} \\ &&n= \text{Sample size} \\ &&\sum \limits_{i=1}^n{x_i} = \text{Sum of of the data values } (x_1,\ldots,x_n). \end{split} \end{equation}

Data Types

There are various types of data, including:

Discrete Quantitative data: This is numeric data which can only take countable values (often within a certain range). For example, the number of questions correct in an exam, people's age in years, number of employees, production run totals.

Qualitative data: This is data which can be observed but is difficult to measure as it is non numeric/ Examples include colour, taste or smell. non numeric and often hard to measure.

Continuous Quantitative data: These are numeric values which can take any numeric value in an interval e.g. height, weight. Note that in practical terms all such data is really discrete as we can only measure to a fixed number of decimal places, but it is often convenient to think of these as continuous and model with continuous distributions.

Summary Statistics

When we only have grouped data (i.e. data already split into class intervals) and so do not know the exact values of the data items (only which class they lie in), we can't calculate the exact mean, mode, median or variance etc. However, you can still make reasonable estimates of these values. This is done using the midpoint of a class interval (so we are effectively assuming that all data values in this interval are the mid point). We then use these values (midpoints) to calculate estimates of the mean and variance in the usual way.

'''For example: ''' suppose that you manage big company that owns 50 different outlets and the sales turnover totals are as follows:

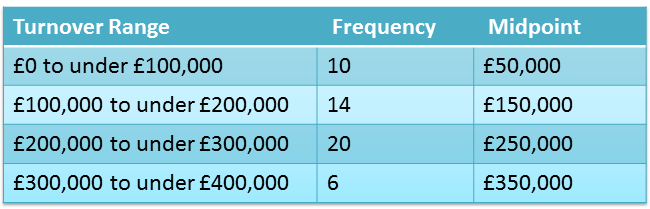
|centre

If you wanted to make an approximation for the mean and variance of the sales turnover in your stores you would do the following calculations:

Firstly you calculate the sum of the data: $\sum x = (10 \times £50,000) + (14 \times £150,000) + (20 \times £250,000)+ (6 \times £350,000) = £ 97,00,000$.

Then you calculate the sum of the squares of the data: $\sum x^2 = (10 \times £50,000^2) + (14 \times £150,000^2) + (20 \times £250,000^2)+ (6 \times £350,000^2) = £ 2.325 \times 10^{12}$

Since the sample size is $50$ we have $n = 50$.

The approximate mean is thus: $\bar x = \dfrac{\sum x}{n} = £19,400$

and the approximate variance is: $ s^2 = \dfrac{\sum x^2 - \frac{(\sum x)^2}{n}}{n-1} = 4.71\times10^{10}$

As you can see we are using the usual formulas but approximating the (grouped) values using the midpoints.

Test Yourself

Test yourself: Calculate measures of central tendency and spread