Geometry of a Circle
Definition
The distance around the boundary of a circle is called the circumference.

The distance across a circle through the centre is called the diameter.
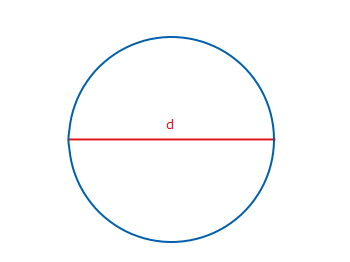
The distance from the centre of a circle to any point on the boundary is called the radius. The radius is half of the diameter; $2r=d$.

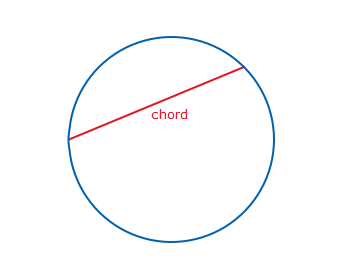
The line segment that joins two points on the circle is a chord. Every diameter is a chord, but not every chord is a diameter.
The area that a chord cuts off is called a segment.

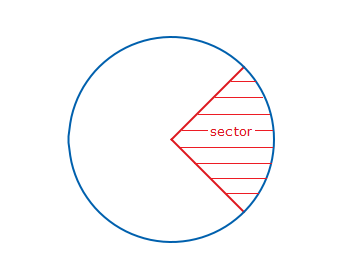
The area inside a circle and bounded by two radii is a sector.
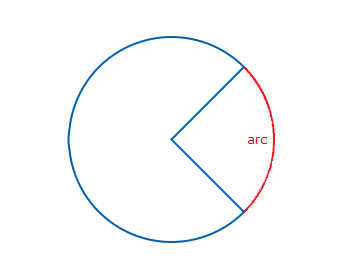
The length between two points around the circumference of a circle is an arc.
Circumference
Definition
The formula for calculating the circumference is \[C = \pi d \qquad\text{or } \qquad C = 2\pi r\] where $d$ is the diameter and $r$ is the radius.
Worked Examples
Example 1
The radius of a given circle is $r=4$cm. Calculate the circumference.
Solution
\begin{align} C &= 2\pi r\\ &= 2 \times \pi \times 4\\ &= 8 \pi \\ &\approx 25.1 \text{cm (to 1 decimal place)} \end{align}
Example 2
Find the diameter of a circle with circumference $18$cm.
Solution
\begin{align} C&=\pi d\\ 18 &= \pi d \end{align} Divide both sides by $\pi$: \begin{align} \frac{18}{\pi} &= d \\ d &= \frac{18}{\pi}\\ d &\approx 5.7 \text{cm (to 1 decimal place)} \end{align}
Area
Definition
The area of a circle with radius $r$ is \[\text{Area }=\pi r^2\]
Worked Examples
Example 1
The radius of a given circle is $2.5$cm. Find the area of the circle.
Solution
\begin{align} \text{Area }&=\pi r^2\\ &=\pi \times 2.5^2\\ &= 6.25\pi \\ &\approx 19.6 \text{cm² (to 1 decimal place)} \end{align}
Example 2
The area of a circle is $50$cm². Find the radius.
Solution
\begin{align} \text{Area }&=\pi r^2\\ 50 &= \pi \times r^2 \end{align} Divide both sides by $\pi$. \begin{align} r^2 &= \frac{50}{\pi}\\ r &= \sqrt{\frac{50}{\pi} }\\ r &\approx 4.0 \text{cm (to 1 decimal place)} \end{align}
Workbook
This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.
See Also
External Resources
- The geometry of a circle workbook at mathcentre.