Inverse Functions

Definition

The inverse of the function $f$ is the function that maps each $f(x)$ back to $x$. We denote the inverse of $f$ by $f^{-1}$. Geometrically, the inverse of a function is the reflection in the line $y=x$.

To determine its inverse, let the function $f(x)$ equal to $y$. Rearrange the function to make $x$ the subject. Then re-write the function replacing $x$ with $f^{-1}(x)$, and $y$ with $x$.

When defining an inverse function, it is important to ensure you also define both its domain and range.

Worked Examples

Example 1

Find the inverse function of $f(x) = 3x+2$.

Solution

Set $y=f(x)$ and rearrange to make $x$ the subject.

\begin{align} y &= 3x+2\\\\ y-2 &= 3x\\ x &= \frac{1}{3}(y-2) \end{align}

Then replace $x$ with $f^{-1}(x)$ and $y$ with $x$

So the inverse is

\[f^{-1}(x) = \dfrac{1}{3}(x-2)\]

This graph shows the lines $f(x) = 3x+2$ in red, and $f^{-1}(x) = \dfrac{1}{3}(x-2)$ in blue. The dotted line is $y=x$.

Example 2

Find the inverse function of $f(x) = 4 - \dfrac{5}{x}$.

Solution

Set $y = f(x)$ and make $x$ the subject.

\begin{align} y &= 4 - \frac{5}{x}\\\\ xy &= 4x - 5\\\\ xy-4x &= -5\\\\ x(y-4) &= -5\\ x &= -\frac{5}{y-4} \end{align}

Then replace $x$ by $f^{-1}(x)$ and $y$ by $x$.

So the inverse is

\[f^{-1}(x) = -\dfrac{5}{x-4}\]

This graph shows the lines $f(x) = 4 - \dfrac{5}{x}$ in red, and $f^{-1}(x) = \dfrac{5}{x-4}$ in blue. The dotted line is $y=x$.

Example 3

Find the inverse of the function $f(x) = x^2 -1$.

Solution

Set $y=f(x)$ and make $x$ the subject.

\begin{align} y &= x^2 -1\\ y +1 &= x^2\\ x &= \sqrt{y+1} \end{align}

Then replace $x$ with $f^{-1}(x)$ and $y$ with $x$.

So the inverse is

\[f^{-1}(x) = \sqrt{x+1}\]

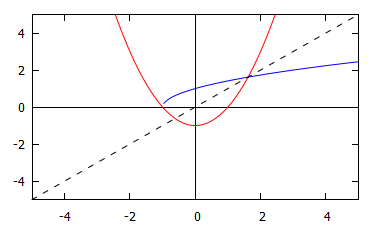
This graph shows the curves $f(x) = x^2-1$ in red, and $f^{-1}(x) = \sqrt{x+1}$ in blue. The dotted line is $y=x$.

Video Example

Prof. Robin Johnson finds the inverse of the function $f(x) = 2 - \dfrac{1}{x}$.

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

External Resources