Linear Functions
Definition
A linear function is a function of the form $f(x) = ax + b$, where $a$ and $b$ are real numbers. Here, $a$ represents the gradient of the line, and $b$ represents the $y$-axis intercept. It is linear as the variable $x$ is of power one.

If we fix $a$ and vary $b$, all the functions will have the same gradient, but they will intercept the $y$-axis at different points.

|center|300px
If we fix $b$ and vary $a$, all the functions pass through the same point on the $y$-axis but have different gradients.

|center|300px
If $a=0$, we just have $f(x) = b$ which has zero gradient, i.e. a horizontal line, which intercepts the $y$-axis at $b$.
Piecewise Linear Functions
A piecewise function is one that is defined by multiple subfunctions, each of which only applies over a particular interval. For example:
$f(x) = \begin{cases} \begin{align} 2x+3, &\text{ if } x\leq -2\\ x+1, &\text{ if } -2\lt x\lt 2\\ 2x-1, &\text{ if } x\geq 2\\ \end{align} \end{cases}$
Notice how there exists a clearly defined interval for each subfunction. When plotted, a piecewise linear function is composed of a series of straight line sections.

|center|400px
Modulus Function
The modulus, or absolute value function, is perhaps the most famous example of a piecewise function. For any real number $x$ the absolute value or modulus of $x$ is denoted by $\vert x \vert$ and defined as \[\vert x \vert = \begin{cases} \begin{align} x, &\text{ if } x \geq 0\\ -x, &\text{ if } x \lt 0 \end{align} \end{cases}\]
This can also be applied to a function. For example: $f(x) = \vert 3x-4 \vert = \begin{cases} \begin{align} 3x-4, &\text{ if } 3x-4 \geq 0\\ -(3x-4), &\text{ if } 3x-4 \lt 0 \end{align} \end{cases}$
Worked Examples
Example 1
Plot the functions:
a) $f(x) = 2x+3$
b) $f(x) = 2x+1$
c) $f(x) = 2x-3$
Solution
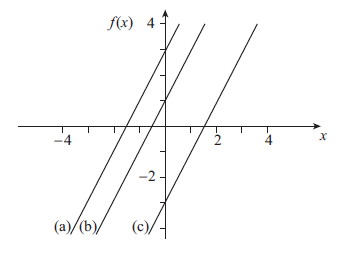
Example 2
Plot the functions:
a) $f(x) = x+2$
b) $f(x) = 2x+2$
c) $f(x) = -2x+2$
d) $f(x) = -x+2$
Solution

Video Examples
Example 1
Prof. Robin Johnson sketches the function $y= x + \vert x \vert -1$.
Workbook
This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.
See Also
External Resources
- Introduction to functions workbook at mathcentre.
- Linear functions workbook at mathcentre.