Simple and Compound Interest (Finance)
Simple and Compound Interest
A capital amount, $C$, grows when interest is earned on it. The amount of interest earned depends on whether simple or compound interest is earned. The accumulated interest amount, $Z$ (=capital+interest earned), is given by \begin{align} &\textbf{SI: }C(1+ni)=Z\\ &\textbf{CI: }C(1+ni)^n=Z \end{align}
where
- $i=$interest rate ($\%$)
- $n=$ the number of years over which interest is earned.
Worked Example 1
Worked Example
What is the accumulated value if you put $£1000$ in a savings account for two years at a rate of $2%$ per annum if:
a) The account pays simple interest?
b) The account pays compound interest?
Solution
Here the initial capital, $C$, is $£1000$, the rate, $i$, is $2\%$ and the number of years, $n$, is $2$.
a) Substituting in these values into the general formula for simple interest: \begin{align} &1000(1+(2\times0.02))\\ &=£1040. \end{align}
So, putting $£1000$ in a savings account for two years at a rate of $2\%$ (simple interest) earns an interest of $£40$ ($1000^2 \times 0.02$).
b) Substituting the above value into the general formula for compound interest: \begin{align} &1000(1+0.02)^2\\ &=£1040.40 \end{align}
So, putting $£1000$ in a savings account for two years at a rate of $2\%$ (compound interest) earns an interest of $£40.40$.
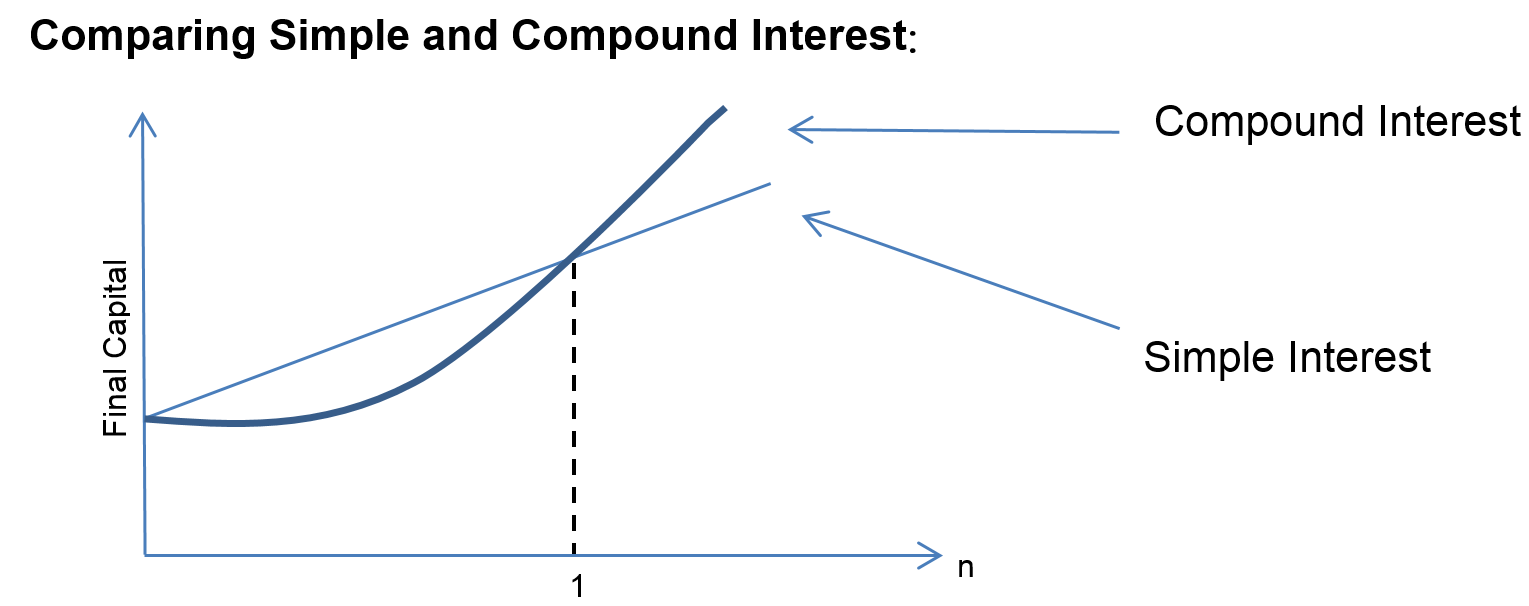
It can be seen that between times $0$ and $1$, simple interest pays more that compound interest but after time $1$ compound interest pays more.
Compound interest is consistent, which means that the interest that a capital earns over a certain period is the same when it is computed over the whole period in one go as when it is first computed over part of the period and then over the remainder. With simple interest, a capital earns more interest if it is first computed over part of the period and then over the remainder, which means that when depositing money it is advantageous to switch account often in order to earn more interest.
Worked Example 2
Worked Example
How long does it take for $£900$ to accumulate to $£1000$ under an interest rate of $4\%$ per annum if:
a) The account pays simple interest?
b) The account pays compound interest?
Solution
Here, the initial capital, $C$, is $£900$, the accumulated value, $Z$, is $£1000$ and the rate, $i$, is $4\%$.
a) Substituting in these values into the general formula for simple interest:
\[900(1+0.04n)=1000.\]
Re-arranging and making $n$ the subject of the formula gives: \begin{align} &n=\frac{1}{0.04}\left(\frac{10}{9}-1\right)\\ &\Rightarrow n \approx 2.78 \text{ years} \end{align}
Substituting in these values into the general formula for compound interest: \[900(1+0.02)^n=1000.\] Re-arranging and making n the subject of the formula gives: \begin{align} &n\ln(1.02)=\ln\left(\frac{10}{9}\right)\\ &\Rightarrow n=\frac{\ln(\frac{10}{9})}{\ln(1.02)}\\ &\Rightarrow n \approx 2.69 \text{ years} \end{align}