Numeracy, Maths and Statistics - Academic Skills Kit

Inverse Functions (Economics)

ContentsToggle Main Menu 1 Inverse Functions 2 Finding the Inverse Function 3 Graphing the Inverse Function 4 Worked Example 5 Video Example 6 Workbook 7 External Resources

Inverse Functions

An inverse function “undoes” the work of a function. We typically denote inverse of the function $f(x)$ by $f^{-1}(x)$ .

For example, if a function $f(x)$ added $2$ to $x$ and then squared the result, the corresponding inverse function $f^{-1}(x)$ would take the square root of $x$ and then subtract $2$ : $f(x)=(x+2)^2$ $f^{-1}(x)=\sqrt{x}-2$

Because the inverse of a function does the opposite to the function, if we apply a function and then apply its inverse, we should get back the original value: For example, consider the function $g(x)=10x$ . The inverse of this function is $g^{-1}(x)=\frac{x}{10}$ . Applying $g$ to $x$ and then $g^{-1}$ gives: $\dfrac{10x}{10}=x$

Note: The $-1$ in $f^{-1}(x)$ is not a power.

Finding the Inverse Function

For example, suppose we want to find the inverse of the function $f(x)=x^2-1$ . We can do this using the following three steps:

1) Replace $f(x)$ with $y$ .

2) Swap the independent variable $x$ with the dependent variable $y$ . This gives $x=y^2-1$ .

3) Rearrange the function to make dependent variable $y$ the subject. This gives $y=\sqrt{x+1}$ .

4) Finally, replace $y$ with $f^{-1}(x)$ . The inverse of $f(x)=40x-9$ is therefore $f^{-1}(x)=\sqrt{x+1}$

Graphing the Inverse Function

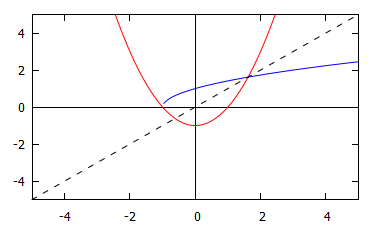
We can draw the graph of the inverse of a function by reflecting the graph of the function in the diagonal line $y=x$ . The graph below shows the curves $f(x) = x^2-1$ in red, and $f^{-1}(x) = \sqrt{x+1}$ in blue. The dotted line is $y=x$ .

Worked Example

Question

Find the inverse function of $f(x) =4-\dfrac{5}{x}$ . Plot the function and its inverse in the same graph.

Solution

Following the above steps, we have:

1) $y=4-\dfrac{5}{x}$

2) $x=4-\dfrac{5}{y}$

3) $\begin{align} x&=4-\dfrac{5}{y}\\ \Rightarrow x&+\dfrac{5}{y}=4\\ \Rightarrow \dfrac{5}{y}&=4-x\\ \Rightarrow \dfrac{y}{5}&=\dfrac{1}{4-x}\\ \Rightarrow y&=\dfrac{5}{4-x}\\ \end{align}$

4) $f^{-1}(x) = -\dfrac{5}{x-4}$

This graph shows the lines $f(x) = 4 - \dfrac{5}{x}$ in red, and $f^{-1}(x) = \dfrac{5}{x-4}$ in blue. The dotted line is $y=x$ .

Video Example

Prof. Robin Johnson finds the inverse of the function $f(x) = 2 - \dfrac{1}{x}$ .

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

One-to-one and inverse functions

External Resources

Inverse functions workbook at mathcentre.

Inverse Functions by Maths is Fun