Projectiles (Mechanics)
Definition
A projectile is any object upon which the only force is gravity.
Worked Example: Resolving the Velocity
Worked Example
Find the horizontal and vertical components of a ball being thrown into the air at an angle of $50^{\circ}$ to the ground at a speed of $30\mathrm{ms^{-1} }$.
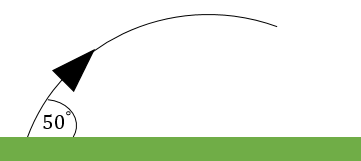
Solution
We find the components using trigonometry. To find the horizontal component, $v_h$, we multiply the velocity by $\cos$ of the angle \begin{align} v_h &= v \times \cos \theta,\\ &= 30 \times \cos 50,\\ &=19.28 \mathrm{ms^{-1} } \text{ (to }2\text{ d.p.).} \end{align} Then to find the vertical component, $v_v$, we multiply the velocity by $\sin$ of the angle \begin{align} v_v &= v \times \sin \theta,\\ &= 30 \times \sin 50,\\ &= 22.98 \mathrm{ms^{-1} } \text{ (to }2\text{ d.p.).} \end{align} Hence the horizontal component of the velocity is $19.28\mathrm{ms^{-1} }$ and the vertical component is $22.98\mathrm{ms^{-1} }$.
Note: You can check your answers using . \begin{align} a^b + b^2 &= c^2,\\ 19.28^2 + 22.98^2 &\approx 900,\\ &\approx 30^2. \end{align}
Using the resolved velocity
We can use the resolved velocity to calculate values for the greatest height, the range and time of flight. The vertical motion has constant acceleration, $9.8\mathrm{ms^{-2} }$, due to gravity. Whereas the horizontal motion is at constant speed.
Worked Examples: Projectiles
Worked Example: Find the Greatest Height
A particle is projected from a point $O$ on a horizontal plane at a speed of $15\mathrm{ms^{-1} }$ with an elevation of $30^{\circ}$. Find the greatest height in $\mathrm{m}$ above the plane reached by the particle.
Solution
With most questions of this type it is generally best to draw a schematic of what is happening in the question.
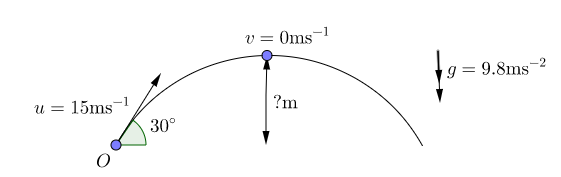
Here we see that the particle was projected with a velocity $u=15\mathrm{ms^{-1} }$ at an angle $30^{\circ}$. The acceleration due to gravity is acting down at a rate of $9.8\mathrm{ms^{-2} }$. When the particle is at its maximum height it is moving neither up nor down so we have $v=0$.
To answer this question we first need to find the vertical component of $u$: \[u_v = 15\cos(30^{\circ}) = 13 \mathrm{ms^{-1} }.\] Since we know the values of $a$, $v$ and $u$, we use one of the SUVAT equations to find $s$. The SUVAT equation we want to use here is: \[v^2 = u^2 + 2as.\] Substituting in the known values gives us \[0 = 13^2 + 2 \times -9.8 \times s.\] Note: Notice that the acceleration has been entered as -ve. This is because the acceleration is acting in the opposite direction to the direction of the particle. Therefore we have \begin{align} 19.6s &= 13^2,\\ s &= 8.62 \mathrm{m} \text{ (to }2\text{ d.p.).} \end{align} The maximum height reached is $8.62\mathrm{m}$.
Worked Example: Find the horizontal distance travelled
A particle is thrown from a point, $O$, which is $30\mathrm{m}$ above flat ground. It is thrown with a speed of $14\mathrm{ms^{-1} }$ at an angle of $25^{\circ}$ to the horizontal. The particle lands at a point $L$. Find the horizontal distance $d\mathrm{m}$ between $O$ and $L$.
Solution
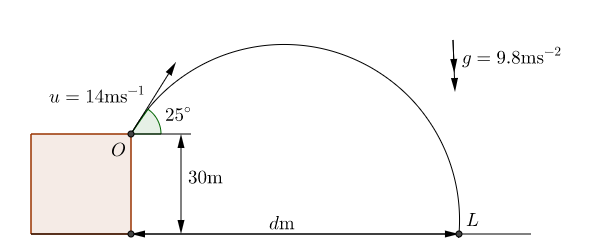
The diagram above shows all the information we know from the question.
This question has to be answered in two parts: 1) Find the time, $t$, taken for the particle to reach $L$. 2) Using $t$ find the horizontal distance travelled, $d$.
To find the time taken we use the SUVAT equations. From the question we know \begin{align} s &= -30,\\ u &= 14\sin(25^{\circ}),\\ v &= ?\\ a &= -9.8,\\ t &= ? \end{align} Note: The $s$ value has been entered as negative because from the point, $O$, where the particle starts to the point, $L$, where the particle finishes, the particle moves downwards.
Since we are trying to find $t$ and we know the variables $s, u$ and $a$ we need to use the SUVAT equation: \[s = ut + \frac{1}{2}at^2.\] Substituting in the values we know gives: \begin{align} s &= ut + \frac{1}{2}at^2,\\ -30 &=14\sin(25^{\circ})t - \frac{1}{2}\times 9.8 \times t^2.\\ \end{align} This can be rearranged to make the right-hand side equal to $0$ and then solved using the quadratic formula \begin{align} 4.9t^2-14\sin(25^{\circ})t-30=0,\\ \Rightarrow t = 3.151\mathrm{s} \text{ and }t = -1.943 \mathrm{s}. \end{align} Since time cannot be negative, we take $t=3.151\mathrm{s}$.
Now that we know how long the particle takes to reach $L$ we can work out the horizontal distance travelled, $d$.
Horizontally there is no acceleration so we can use \[d = vt.\] Substituting in the values of $v$ and $t$ gives \begin{align} d &= 14\cos(25^{\circ}) \times 3.151,\\ &= 40.00\mathrm{m} \text{ (to }2\text{ d.p.).} \end{align} Therefore the particle travels $40\mathrm{m}$ in the horizontal plane to reach $L$.
Test Yourself
Coming soon.