Statics of a particle (Mechanics)
Statics of a particle
To solve problems about particles in equilibrium we resolve the forces horizontally and vertically.
A particle is said to be in equilibrium if motion does not take place when it is acted upon by two or more forces. Therefore the resultant force is zero and the particle remains at rest or remains stationary.
For problems involving friction we use the relationship $F \leq \mu R$.
Worked Example: A particle in equilibrium
Find the magnitude of the unknown forces
The diagram shows a particle in equilibrium under the forces shown.

Find the magnitude of the forces $F_1$ and $F_2$.
Solution
To find the magnitude of the forces we resolve both vertically and horizontally. Horizontally, with the positive direction being $\left( \rightarrow \right)$ we have \begin{align} 8 \cos(65^{\circ}) + F_1 \cos((180 - 45)^{\circ}) & = 0, \\ 8 \cos(65^{\circ}) + F_1 \cos (135^{\circ}) & = 0, \\ F_1 & = \frac{ - 8 \cos (65^{\circ}) } {\cos (135^{\circ}) }, \\ & = 4.781\mathrm{N} \text{ (to 3 d.p.).} \end{align} Note that here we could have used $ - F_1 \cos (45^{\circ})$ instead of $F_1 \cos (135^{\circ})$ as they give the same result. We have equated the sum of the forces to zero as there is no resultant force due to equilibrium.
Vertically, with the positive direction being upwards, we have \begin{align} F_1 \cos ((90 - 45)^{\circ}) + 8 \cos ((90 - 65)^{\circ}) - F_2 & = 0, \\ 4.781 \cos (45^{\circ}) + 8 \cos (25^{\circ}) & = F_2, \\ F_2 & = 10.631 \mathrm{N} \text{ (to 3 d.p.).} \end{align} Note that here we could have used $ \sin \theta^{\circ}$ instead of $ \cos(90 - \theta)^{\circ}$ for a given $\theta$ as these give the same result.
When the particle is on an incline
The diagram shows a particle in equilibrium under the forces shown.
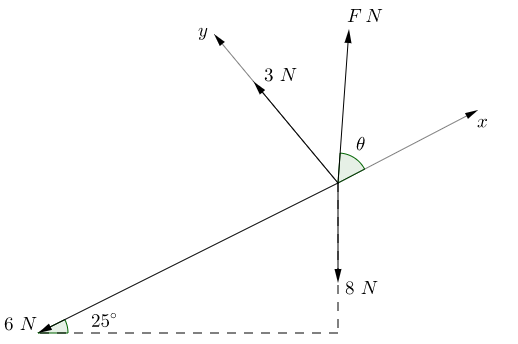
Find the magnitude of the force $F$ and the magnitude of the angle $\theta$.
Solution
We resolve up the plane, taking the direction up as the positive (shown as the $x$-direction in the diagram). \begin{align} F \cos \theta - 6 + 5 \cos ((90 + 25)^{\circ}) & = 0, \\ F \cos \theta & = 6 - 5 \cos (115^{\circ}), \\ & = 8.113 \mathrm{N} \text{ (to 3d.p.).} \end{align} We resolve perpendicular to the plane (shown as the $y$-direction in the diagram). \begin{align} F \cos (90^{\circ} - \theta) + 3 + \cos (180 - 25)^{\circ} & = 0, \\ F \sin \theta + 3 + 8 \cos (155^{\circ}) & = 0, \\ F \sin \theta & = - 3 - 8 \cos (155^{\circ}), \\ & = 4.250 \text{ (to 3d.p.).} \end{align} We can then divide the second equation by the first to give \begin{align} \tan \theta & = \frac{4.25}{8.113}, \\ & = 0.524 \text{ (to 3d.p.),} \\ \theta & = 27.648^{\circ} \text{ (to 3d.p.).} \end{align} From this we can find $F$ \begin{align} F \cos \theta & = 8.113, \\ F & = \frac{8.113}{\cos (27.648^{\circ}) }, \\ & = 9.159 \mathrm{N} \text{ (to 3d.p.).} \end{align}
Worked Example: Additional forces acting on a particle in equilibrium
Find the tension in the strings
A particle of $8 \mathrm{kg}$ is suspended by two light inextensible strings that are inclined at the angles shown in the diagram below.
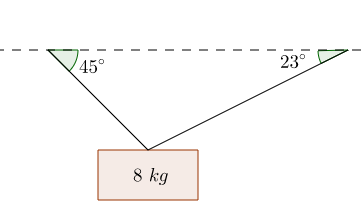
Find the tension in the strings when the particle is in equilibrium.
Solution
To find the tensions in the strings we can model the particle as follows
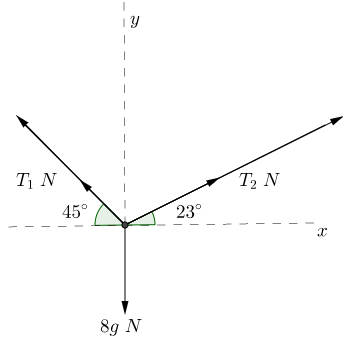
remembering to include the weight of the particle. We then resolve the forces to find $T_1$ and $T_2$. First we can resolve in the upward direction (shown by the $y$-axis in the diagram). \begin{align} T_2 \cos (90 - 23)^{\circ} + T_1 \cos (90 - 45)^{\circ} - 8g & = 0, \\ T_2 \cos (67^{\circ}) + T_1 \cos (45^{\circ}) - 78.4 & = 0, \\ T_1 & = \frac{78.4 - T_2 \cos (67^{\circ})}{\cos (45^{\circ}) }. \end{align} We then resolve in the direction $\left( \rightarrow \right)$ (shown by the $x$-axis in the diagram) and substitute in our value for $T_1$. \begin{align} T_1 \cos (180 - 45)^{\circ} + T_2 \cos (23^{\circ}) + 8g \cos (90^{\circ}) & = 0, \\ T _1 \cos (135^{\circ}) + T_2 \cos (23^{\circ}) & = 0, \\ \frac{78.4 - T_2 \cos (67^{\circ}) } {\cos (45^{\circ}) } \cos (135^{\circ}) + T_2 \cos (23^{\circ}) & = 0, \\ \frac{78.4}{\cos (45^{\circ }) } \cos (135^{\circ}) - T_2 \frac{\cos (67^{\circ}) }{\cos (45^{\circ}) } \cos (135^{\circ}) + T_2 \cos (23^{\circ}) & = 0, \\ T_2 \left( \cos(23^{\circ}) - \frac{\cos(67^{\circ}) } {\cos(45^{\circ}) } \cos(135^{\circ}) \right) & = - \frac{78.4}{\cos (45^{\circ}) } \cos (135^{\circ}), \\ 1.311 T_2 & = 78.4, \\ T_2 & = 59.802 \mathrm{N} \text{ (to 3d.p.).} \end{align} We can then substitute our $T_2$ value back into the first equation to find $T_1$. \begin{align} T_1 & = \frac{78.4 - T_2 \cos (67^{\circ}) }{\cos (45^{\circ}) }, \\ & = \frac{ 78.4 - 59.802 \cos (67^{\circ}) } {\cos (45^{\circ}) }, \\ & = 77.829 \mathrm{N} \text{ (to 3 d.p.).} \end{align}
Worked Example: Statics involving friction
Limiting equilibrium
A mass of $6 \mathrm{kg}$ rests on a rough horizontal plane. The coefficient of friction between the mass and the plane is $\mu=0.6$. Find the magnitude of the maximum force $P \mathrm{N}$ which acts on the mass without causing it to move if the force $P$ is horizontal. What is the force $P$ acts at an angle of $75^{\circ}$ above the horizontal.
Solution
This is an example of limiting equilibrium as we are asked for the maximum force before movement takes place. We resolve the forces in the upwards direction. \begin{align} F & = ma, \\ R - mg & = m \times 0, \\ R & = mg, \\ & = 6 \times 9.8, \\ & = 58.8 \mathrm{N}. \end{align} Friction, $F$, is limiting so \begin{align} F & = \mu R, \\ & = 0.6 \times 58.8, \\ & = 35.28 \mathrm{N}. \end{align} We can then resolve in the horizontal direction, where friction acts in the opposite direction to the force $P$. \begin{align} P - F & = 0, \\ P & = F, \\ & = 35.28 \mathrm{N}. \end{align} So when $P$ is applied horizontally the maximum value it can be is $35.28 \mathrm{N}$.
When $P$ acts an angle of $75^{\circ}$ above the horizontal we can draw a diagram as below.
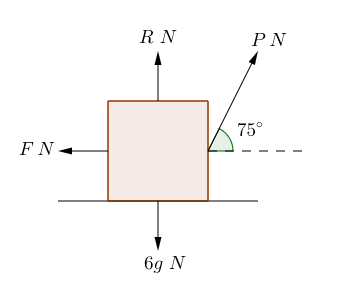
Again this is in limiting equilibrium, we can resolve vertically \begin{align} R + \cos(90 - 75)^{\circ} - 6g & = 0, \\ R & = 6g - P \cos (15^{\circ}), \\ & = 58.8 - P \cos(15^{\circ}). \end{align} As friction is limiting, $F = \mu R$ where $\mu = 0.6$ \begin{align} F & = \mu R, \\ & = 0.6 \times \left(58.8 - P \cos (15^{\circ}) \right). \end{align} Now resolving horizontally \begin{align} P \cos (60^{\circ}) - F & = 0, \\ P \cos (60^{\circ}) & = F, \\ & = 0.6 \times \left( 58.8 - P \cos (15^{\circ}) \right), \\ & = 35.28 - 0.6P \cos (15^{\circ}), \\ P ( \cos (60^{\circ}) + 0.6 \cos (15^{\circ}) ) & = 35.28, \\ P & = \frac{35.28} { \cos (60^{\circ}) + 0.6 \cos (15^{\circ}) }, \\ & = 32.680 \mathrm{N} \text{ (to 3d.p.).} \end{align} So when $P$ acts an angle of $75^{\circ}$ above the horizontal the maximum value it can be is $32.680 \mathrm{N}$.
Test Yourself
Try our Numbas test on statics of a particle: Statics of a Particle