Vectors using Line segments(Mechanics)
Vectors using line segments
A vector can be seen as a directed line segment, where the direction of the vector is represented by the direction of the line and the magnitude of the vector is represented by the length of the line.
The vector which describes the displacement of $B$ from $A$ is written usually as AB, $\vec{AB }$ or $\overline{AB}$. Or if a single letter represents a vector it is usually underlined or bold.
If two vectors have the same direction and magnitude they are said to be equal.
If two vectors have the same direction they are said to be parallel.
Vectors can be added using the triangle law of addition \begin{equation} \vec{A C} = \vec{AB} + \vec{B C}. \end{equation}
Worked Example: Parallelogram
Vectors
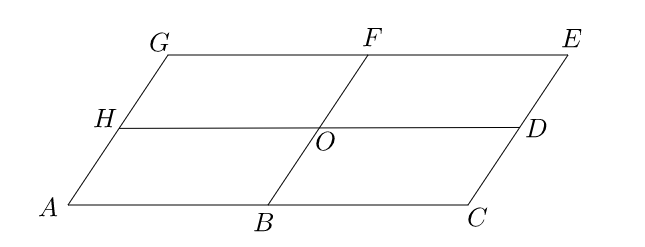
Consider the parallelogram below where the points $F,H,D$ and $B$ are the mid-points of the sides and $O$ is the centre. Suppose that $\vec{AG} =$ a and $\vec{A C} = $ b. What are the vectors $\vec{AE}, \vec{GC}, \vec{FE}, \vec{ED}$ and $\vec{FD}$ in terms of a and b.
Solution
We can use the triangle rule for addiction of vectors to represent \begin{align} \vec{AE} & = \vec{A C} + \vec{CE}, \\ & = \vec{A C} + \vec{AG}, \\ & = \mathbf{b} + \mathbf{a}, \\ & = \mathbf{a} + \mathbf{b}. \end{align} Here we have used that opposite sides to the parallelogram are parallel and equal in length, so $\vec{CE} = \vec{AG}$. \begin{align} \vec{GC} & = \vec{GA} + \vec{A C}, \\ & = - \vec{AG} + \vec{A C}, \\ & = - \mathbf{a} + \mathbf{b}, \\ & =\mathbf{b} - \mathbf{a}. \end{align} Here we have used that $\vec{GA}$ is equal in length to $\vec{AG}$ but is in the opposite direction. \begin{align} \vec{FE} & = \vec{AB}, \\ & = \frac{1}{2} \vec{A C}, \\ & = \frac{1}{2} \mathbf{b}. \end{align} Here we have used that because we have a parallelogram $\vec{ A C} = \vec{G E}$ and because $B$ and $F$ are the mid-points of $A C$ and $G E$ respectively we have that $\vec{AB} = \vec{B C} = \vec{GF} = \vec{FE} = \frac{1}{2}$b. \begin{align} \vec{ED} & = \frac{1}{2} \vec{EC}, \\ & = \frac{1}{2} \vec{GA}, \\ & = \frac{1}{2} (- \mathbf{a}), \\ & = - \frac{1}{2} \mathbf{a}. \end{align} Here we have used similar arguments to use the other parallel sides of the parallelogram to find $\vec{ED}$. \begin{align} \vec{FD} & = \vec{FE} + \vec{ED}, \\ & = \frac{1}{2} \mathbf{b} - \frac{1}{2}\mathbf{a}, \\ & = \frac{1}{2} (\mathbf{b} -\mathbf{a}). \end{align} Therefore $\vec{FD} = \frac{1}{2}(\mathbf{b} - \mathbf{a}) = \frac{1}{2} \vec{GC}$, so $FD$ is parallel to $GC$ and half as long.
Worked Example: Triangle
:Vectors
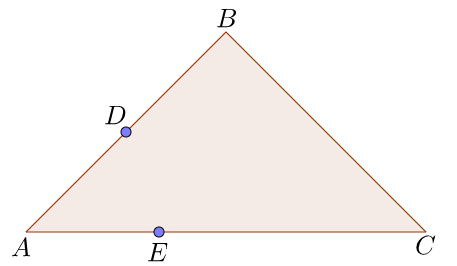
Consider the triangle below where $D$ is the mid-point of $A B$ and $E$ divides $A C$ in the ratio $1:2$. Suppose that $\vec{A D} = $ a and that $\vec{B C} =$ b. What is $\vec{B E}$ in terms of a and b?
Solution
We have that \begin{align} \vec{B E} & = \vec{B A} + \vec{A E}, \\ & = - \vec{A B} + \frac{1}{3} \vec{A C}, \\ & = - 2 \mathbf{a} + \frac{1}{3} \left( \vec{A B} + \vec{ B C} \right), \\ & = - 2 \mathbf{a} + \frac{1}{3} \left( 2 \mathbf{a} + \mathbf{b} \right), \\ & = - \frac{4}{3} \mathbf{a} + \frac{1}{3} \mathbf{b}, \\ & = \frac{1}{3} \left( \mathbf{b} - 4 \mathbf{a} \right). \end{align}