Solution

The distance walked is $5\mathrm{km} + 6\mathrm{km} = 11\mathrm{km}$.

This is not the same as the distance from $X$ to $Z$, we can represent the journey on a diagram as shown below.

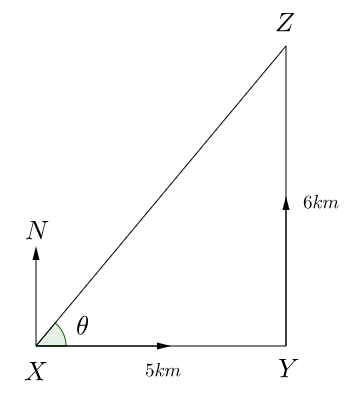
Now \begin{align} XZ^2 & = XY^2 + YZ^2, \\ & = 5^2 + 6^2, \\ & = 61, \\ XZ & = 7.81 \mathrm{km} \text{ (3s.f.).} \end{align} So the distance $XZ$ is $7.81 \mathrm{km}$ (3s.f.). We have that \begin{align} \tan \theta & = \frac{6}{5} \\ \theta & = 50.2^{\circ} \text{ (3s.f.).} \end{align} So $Z$ is $7.81\mathrm{km}$ from $X$ on a bearing of $50^{\circ}$.

Solution

We can represent the journey on a diagram as shown below.

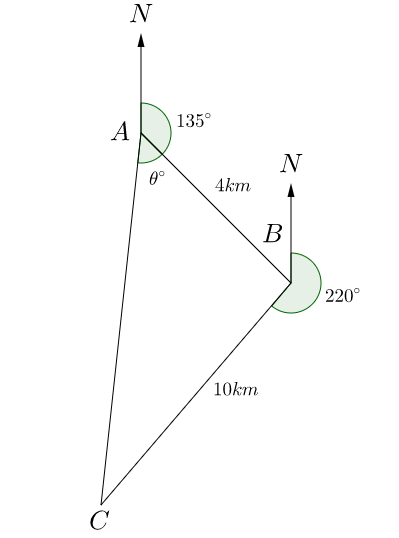
Now we can use the cosine rule \begin{equation} c^2 = a^2 + b^2 - 2ab \cos C \end{equation} in the triangle $A B C$ to get \begin{align} A C^2 & = 4^2 + 10^2 - \left( 2 \times 4 \times 10 \times \cos(95^{\circ}) \right), \\ & = 16 + 100 - 80\cos(95^{\circ}), \\ & = 122.972 \text{ (to 3d.p.)} \\ A C& = 11.089 \mathrm{km} \text{ (to 3d.p.).} \end{align} Note that the angle $90^{\circ}$ has been found by $360 - (220 + (180-135)) = 95$. We can then use the sine rule \begin{equation} \frac{ \sin A}{a} = \frac{ \sin B}{b} = \frac{ \sin C}{c} \end{equation} to get \begin{align} \frac{\sin \theta}{10} & = \frac{\sin(95^{\circ})}{11.089} \\ \sin \theta & = \frac{10 \times \sin(95^{\circ})}{11.089} \\ & = 0.898... \\ \theta & = 63.944^{\circ} \text{ (to 3d.p.)} \end{align} We have that the bearing of $C$ from $A$ is $135 + 63.944 = 198.944^{\circ}$ and that the distance is $11.089\mathrm{km}$.