Simple Linear Regression

Definition

Simple linear regression aims to find a linear relationship to describe the correlation between an independent and possibly dependent variable. The regression line can be used to predict or estimate missing values, this is known as interpolation.

Least Squares Regression Line, LSRL

The calculation is based on the method of least squares. The idea behind it is to minimise the sum of the vertical distance between all of the data points and the line of best fit.

Consider these attempts at drawing the line of best fit, they all look like they could be a fair line of best fit, but in fact Diagram 3 is the most accurate as the regression line has been calculated using the least squares regression line. 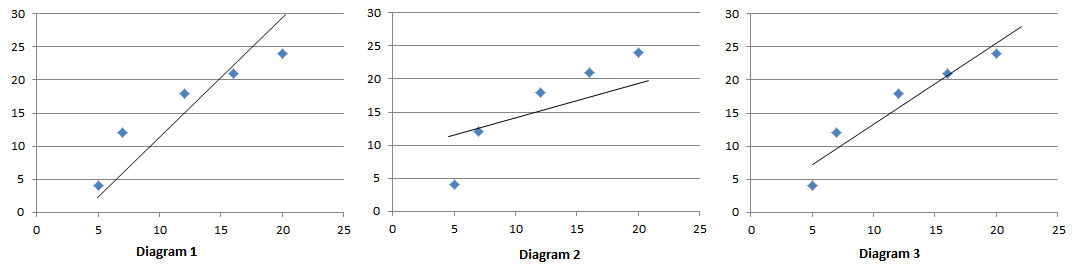|1100 px

The equation of the least squares regression line is \[\displaystyle \hat{y}=a+bx\]

where:

  • $\hat{y}$ is the predicted value of $y$,
  • $\displaystyle a=\bar y-b\bar x$,
  • $\displaystyle b=\frac{S_{xy}}{S_{xx}} = \frac{ \sum(x_i-\bar x)(y_i-\bar y)}{ \sum(x_i-\bar x)^2 }=\frac{ \sum(xy)-\frac{\sum{x} \sum{y}}{n}}{\sum(x^2)-\frac{(\sum{x})^2}{n}}$,
  • $\bar x=\dfrac{\sum{x}}{n}$,
  • $\bar y=\dfrac{\sum{y}}{n}$,

Note: The underlying statistical model here is that there is a linear relation between the variables, say $y = a'+ b'x$, and so we should regard the equation that we obtain using the method above as resulting in an estimate for the true equation. For this reason many authorities write $y = a +bx + \epsilon$ to emphasise this point. A further discussion on the nature of the error $\epsilon$ is not appropriate here, but is covered in the references below.

Worked Examples
Example 1

Consider the example below where the mass, $y$ (grams), of a chemical is related to the time, $x$ (seconds), for which the chemical reaction has been taking place according to the table:

Time, $x$ (seconds)

$5$

$7$

$12$

$16$

$20$

Mass, $y$ (grams)

$40$

$120$

$180$

$210$

$240$

Find the equation of the regression line.

Solution
|250px

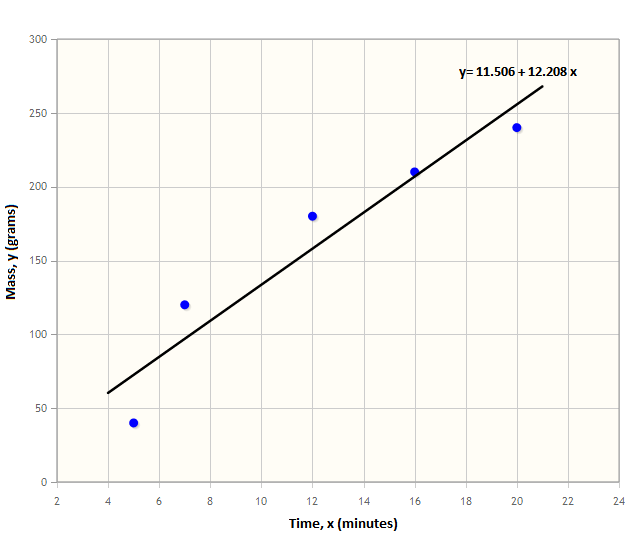
|250px

To work out the regression line the following values need to be calculated: $\displaystyle a=\bar y-b\bar x$ and $\displaystyle b=\frac{S_{xy}}{S_{xx}}$. The easiest way of calculating them is by using a table.

Start off by working out the mean of the independent and dependent variables.

\begin{align} \bar x&=\frac{\sum{x} }{n}\\ &=\frac{5+7+12+16+20}{5}\\ &=\frac{60}{5}\\ &=12,\\ \bar y&=\frac{\sum{y} }{n}\\ &=\frac{40+120+180+210+240}{5}\\ &=\frac{790}{5}\\ &=158. \end{align}

$x_i$

$y_i$

$x_i-\bar x$

$y_i-\bar y$

$(x_i-\bar x)(y_i-\bar y)$

$(x_i-\bar x)^2$

$5$

$40$

$5-12=-7$

$40-158=-118$

$-7 \times -118=826$

$-7^2=49$

$7$

$120$

$7-12=-5$

$120-158=-38$

$-5\times -38=190$

$-5^2=25$

$12$

$180$

$12-12=0$

$180-158=22$

$0 \times 22=0$

$0^2=0$

$16$

$210$

$16-12=4$

$210-158=52$

$4 \times 52=208$

$4^2=16$

$20$

$240$

$20-12=8$

$240-158=82$

$8 \times 82=656$

$8^2=64$

$\sum{x}=60$

$\sum{y} = 790$

$\sum(x_i-\bar x)(y_i-\bar y)=1880$

$\sum{(x_i-\bar x)^2}=154$

Now calculate $b$

\begin{align} b&=\frac{S_{xy} }{S_{xx} }\\ &=\frac{\sum(x_i-\bar x)(y_i-\bar y)}{\sum(x_i-\bar x)^2}\\ &=\frac{1880}{154}=12.20779...\\ &=12.208\ \text{(3.d.p.) } \end{align}

and calculate $a$

\begin{align} a&=\bar y-b\bar x\\ &=158-12.208\times12\\ &=11.506...\\ &=11.506\text{ (3.d.p.).} \end{align}

So the equation of the regression line is: $\hat{y}=a+bx=11.506+12.208x.$

Example 2

To see how students' reaction skills have improved over a year, eight students took a reactions test at the start of the year and at the end of the year. These are their scores:

Student

Liam

Felicity

Adian

Mel

Leroy

Vic

Lawrie

Louise

First Test, $x$

$56$

$75$

$61$

$61$

$67$

$72$

$62$

$61$

Second Test, $y$

$21$

$39$

$34$

$21$

$32$

$24$

$29$

$24$

Find the equation of the regression line given that:

\[\sum{x}=515,\ \sum{y}=224,\ \sum{x^2}=33441,\ \sum{y^2}=6576\ and\ \sum{xy}=14590.\]

Solution

We know that the equation of the least squares regression line is

\[\displaystyle \hat{y}=a+bx.\]

As we have been given some summed values we are going to use $\displaystyle b=\frac{S_{xy}}{S_{xx}} =\frac{ \sum(xy)-\frac{\sum{x} \sum{y}}{n}}{\sum(x^2)-\frac{(\sum{x})^2}{n}}$.

\begin{align} \displaystyle b&=\frac{S_{xy} }{S_{xx} }\\ &=\frac{ \sum(xy)-\frac{\sum{x} \sum{y} }{n} }{\sum(x^2)-\frac{(\sum{x})^2}{n} }\\ &=\frac{14590-\frac{515\times 224}{8} }{33441-\frac{515^2}{8} }\\ &=0.590534...\\ &=0.590\ \text{(3.d.p.)} \end{align}

To find $a$ we need to first work out the mean of $x$ and $y$.

\begin{align} \bar{x}&=\dfrac{\sum{x} }{n}=\frac{515}{8}=64.375,\\ \bar{y}&=\dfrac{\sum{y} }{n}=\frac{224}{8}=28\\ a&=\bar{y}-b\bar{x}\\ &=28-(0.590\times64.375)\\ &=-10.015631...\\ &=-10.016\ \text{(3.d.p.)} \end{align}

So the equation of our regression line is $\hat{y}=-10.106+0.590x$.

Video Example

Alissa Grant-Walker presents a video on working out the linear regression line.

Interpreting the Regression Line

The simple linear regression line, $\displaystyle \hat{y}=a+bx$, can be interpreted as follows:

  • $\hat{y}$ is the predicted value of $y$,
  • $a$ is the intercept and predicts where the regression line will cross the $y$-axis,
  • $b$ predicts the change in $y$ for every unit change in $x$.

We can also use the equation of the regression line for finding approximate values for missing data.

Note: Using this to estimate outside the range of your data is unreliable.

Worked Example
|250px

|250px

Using the data from the last worked example about the mass of a chemical as time increases, we worked out the equation of the regression line to be $\hat{y}=11.506+12.208x$. We can interpret this as for every $1$ minute increase in time the mass of the chemical increases by $12.208$ grams. The equation also tells us that when no time has passed, (when $x$ is zero), the initial mass of the chemical is $11.506$ grams.

Example 1

What is the mass of the chemical after ten seconds has passed?

Solution 1

Take your equation and enter the value of time $x=10$ and calculate $\hat{y}$.

\[\hat{y}=11.506+12.208\times10=133.586.\] This means that after $10$ seconds of our experiment has passed, the mass of the chemical will be $133.586$ grams. Check this value against a scatter plot of our data to see if this answer is reasonable.

Example 2

By how much does the chemical increase in weight in five seconds?

Solution 2

For every minute increase in time the mass of the chemical increases by $12.208$ grams. Multiply $12.208$ grams by $5$ to find the increase in weight of the chemical in $5$ seconds.

\[12.208\times5=61.40 \text{ (grams).}\]

Example 3

How much time does it take for the weight of the chemical to increase by $50$ grams?

Solution 3

We know that for every minute increase in time the mass of the chemical increases by $12.208$ grams, this also means it takes $\frac{1}{12.208}$ seconds for the chemical to increase by $1$ gram. To find the time taken for the chemical to increase in weight by $50$ grams we need to multiply $\frac{1}{12.208}$ by $50$.

\[\frac{1}{12.208}\times 50=4.096\text{ (3 d.p.)} .\]

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

Test Yourself

Test yourself: Numbas test on linear regression

External Resources

See Also