About Sampling
These are some of the basic properties and principles involved in sampling. Sampling is a complex topic with a wide literature, which goes beyond what is appropriate for this wiki site.
Definitions
A sample is a selection (subset) of data from a larger group of data, (called the population.) A sample should be representative of the population, this means the sample and the population should have similar properties.
A population is a particular group of individuals or items. It can be any size or even infinite.
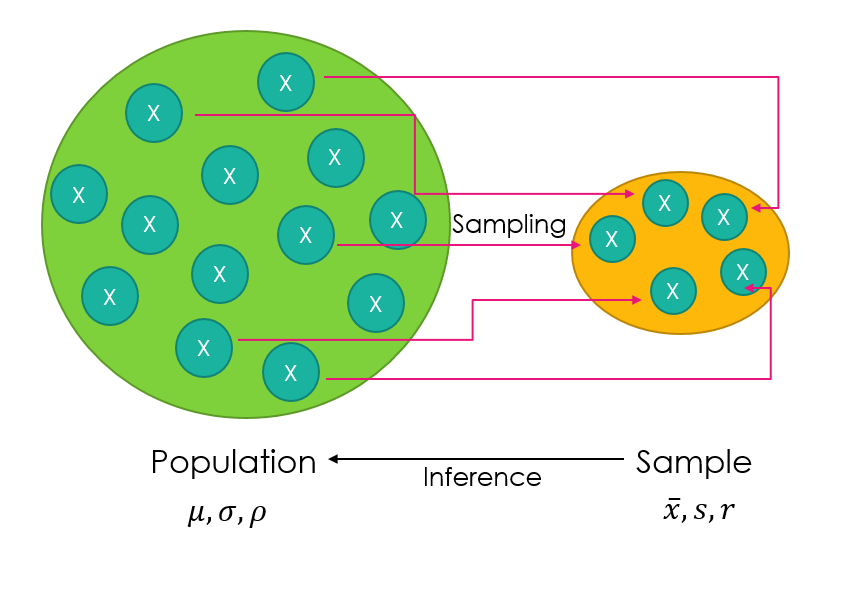
A survey can be collected in two ways:
- Census - A census is where every member of the population is sampled. This is a preffered method of surveying when the population is small, however when the population is large it is often time consuming and expensive to take a census.
- Sample Survey - A sample survey is when less than the whole of the population is surveyed. A sample survey is used when the population you are surveying is large.
Sampling units are the people or items that have been sampled. The target population is the collection of sampling units.
A sampling frame is the set of individuals or items from which a sample has been drawn.
Illustrative Example
In a survey of potential customers for a new service in the population of London. The survey team has drawn $1000$ numbers at random from a telephone directory for the city, made $200$ calls each day from Monday to Friday from 8am to 5pm and asked some questions. In this example, population of interest is all inhabitants of the city; the sampling frame includes only those people in London who have a telephone which is also included in the directory, are likely to be at home from 8am to 5pm from Monday to Friday and do not refuse to answer telephone surveys.
Reasons for Sampling
- We use sampling when the population size is too big and impractical to work with. You can manipulate samples in order to estimate what would happen to the parent population when manipulated in the same way. Note that an estimate of a parameter derived from the sample may be different from the true value.
- Another reason for sampling would be to conduct a hypothesis test.
Before taking a Sample
Before taking your sample the following issues need to be considered:
- Which population parameters we want to estimate.
- How much will taking a sample cost?
- How much you already know. If the experiment has been studied before, use that information to reduce sample size.
- Variability of the population. The more variable the population, the more samples needed.
- How hard is it practically to collect the data?
- How precise you want your estimates to be.
Sampling Process
- Start by defining the population under consideration.
- Define the sampling frame.
- Choose an appropriate sampling method.
- Collect any data you will need to choose your sample.
- Collect the sample.
Properties of Samples
Three factors that might affect how well a sample represents the populations are:
- Sampling procedure - the procedure used to create a sample may be biased. See below.
- Sample size - typically, if you have a larger sample size the error obtained will be smaller as it will be a better representation of the entire population.
- Participation - a poor response rate will adversely affect the value of the sample.
Bias
Bias is when the sample does not fully represent the properties of the population. Reasons for bias include:
- Poor sampling frame - using out-of-date information, not including significant sections of the population.
- Wrong choice of sampling unit - for example asking only male participants.
- Non-response or mis-response of some of the chosen sampling units - it might be difficult to contact or obtain information about particular units. An example of a mis-response is if the questions in a questionnaire are misunderstood, some individuals may have answered the questions incorrectly.
- Inappropriate choice of surveyer - if the person who is conducting the survey asks misleading questions or are purposely phrasing questions to influence the response of the participant.
Sample Size
What to consider before choosing a sample size
- Population size - how many people/items in your population?
- Confidence Interval - how much error do you want to allow?
- Significance levels - Common confidence intervals are $95$% and $99$%.
- Standard of Deviation - How much variance do you expect to obtain? A common choice would be $0.5$ which is equivalent to $50$%.
How to calculate a sample size
For more information about calculating sample size see this resource.
External Resources
- Sample Size at