Z-tests and T-tests (Business)
z-tests - Population variance known
$z$-tests are a statistical way of testing a hypothesis when either:
- We know the population variance $\sigma^2$, or alternatively
- We do not know the population variance but our sample size is large, $n \geq 30$'''. In this case we use the sample variance as an estimate of the population variance.
If we have a sample size of less than $30$ and do not know the population variance then we must use a t-test
These are some further conditions for using this type of test:
- The data must be normally distributed.
- All data points must be independent.
- For each sample the variances must be equal.
One sample z-tests
We use a one sample $z$-test when we wish to compare the sample mean $\mu$ to the population mean $\mu_0$.
Illustrative Example
A headmistress wants to compare the GCSE English results of her pupils against the national data to determine if there is a difference. The national data is normally distributed with known variance. A large number of pupils in her school have taken the exam and in order to save time she decides to take a random sample of her pupils' results. She calculates the sample mean and then uses a $z$-test to asses whether there is a significant difference between the sample mean and the national mean at the 5% significance level. In this case, the null hypothesis would be that there is no significant difference, and the $z$-test is used to see whether or not this is the case. The $z$-test statistic is calculated using the following formula:
\begin{equation} z = \dfrac{\bar{x} - \mu_0}{\sqrt{\dfrac{\sigma^2}{n}}} \end{equation}
The Method:
- Firstly, identify the null hypothesis $H_0: \mu = \mu_0$ for example, the average GCSE English results of a group of schoolchildren is the same as the national average.
- Then identify the alternative hypothesis $H_1$ and decide if it is of the form $H_1: \mu \neq \mu_0$ (a One-tailed test). or if there is a specific direction for how the mean changes $H_1: \mu > \mu_0$ or $H_1: \mu < \mu_0$, (a One-tailed test).
For example, the average GCSE English results of the schoolchildren is higher than the national average (a one-tailed hypothesis), or the average GCSE English results of the schoolchildren is different from the national average (a two-tailed hypothesis).
- Next, calculate the test statistic, using the formula above in the red box.
- Compare the test statistic to the critical values.
- Form conclusions. If your $z$-statistic is greater than the critical values in the table, it is significant so you can reject the null hypothesis at that level. Otherwise you accept it.
See the page of worked examples.
Two sample z-tests
Often, we need to compare the means from two samples and we use the $z$-statistic for when we know the population variances ($\sigma^2$) (see two sample t-tests for unknown variances). There are two types of two sample $z$-test:
- Paired $z$-test/related $z$-test - comparing two equally sized sets of results which are linked (where you test the same group of participants twice or your two groups are similar).
- Independent/unrelated $z$-test - where there is no link between the groups (different independent groups).
The main difference between these two tests is that the $z$-statistic is calculated differently.
For the independent/unrelated $z$-test, the test statistic is:
\begin{equation} z = \dfrac{\bar{x_1} - \bar{x_2}}{\sqrt{\dfrac{\sigma_1^2}{n_1} +\dfrac{\sigma_2^2}{n_2}}} \end{equation}
where $\bar{x_1} \text{and } \bar{x_2}$ are the sample means, $n_1 \text{and } n_2$ are the samples sizes and $\sigma_1^2 \text{and } \sigma_2^2$ are the population variances.
For paired/related $z$-tests the $z$-statistic is:
\begin{equation} z= \dfrac{\bar{d}- D}{\sqrt{\dfrac{\sigma_d^2}{n}}} \end{equation}
where $\bar{d} $is the mean of the differences between the samples, $D$ is the hypothesised mean of the differences (usually this is zero), $n$ is the sample size and $\sigma_d^2$ is the population variance of the differences.
- Once you have calculated the test statistic you use the standard normal tables to obtain the critical values, obtain a range for the $p$-value and compare your $z$-statistic. Then form your conclusions. If the $z$-statistic is significant then you can reject the null hypothesis, otherwise you accept it.
z-Table
This is a $z$-table with an explanation of each section of the table and a guide for using it: 
Worked Example 1
Worked Example - One Sample z-Test
You work in the HR department at a large franchise and you are currently working in the expenses department. You want to test whether you have set your employee monthly allowances correctly. In the past it was believed that the average claim was $£500$ with a standard deviation of $150$, however you believe this may have increased due to inflation. You want to test if the monthly allowances should be increased. A random sample is taken of $40$ employees and gives a mean monthly claim of $£640$.
Perform a hypothesis test of whether you should increase your employees' monthly allowances.
Solution
This is a one sample $z$-test because you know the population standard deviation ($\sigma = 150$). It is also a One-tailed example because we are testing for an increase.
The hypotheses are:
- $H_0: \mu = 500$
- $H_1: \mu > 500$
Calculating the $z$-statistic using the formula above gives: $\dfrac{640 - 500}{~\sqrt{~\dfrac{150^2}{40}~}~} = 5.903$ (to 3 d.p)
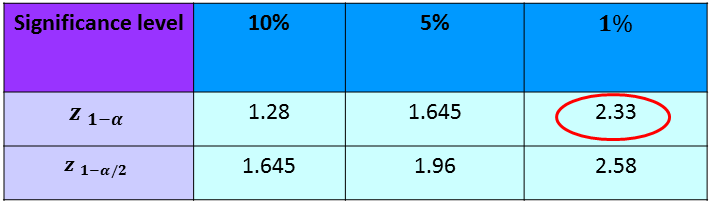
|centre
Next, we look up this value in the $z$-table (see above). Since this is a one tailed example, we compare the values at the $z_{1- \alpha}$ level. At the $1\%$ level, you can see that $ 5.903 > 2.33$, so this is a significant result. This means we have sufficient evidence to reject the null hypothesis that there has been no change in the average employee expenses claim. Thus, you should increase the monthly allowances.
t-tests - Population variance unknown
One Sample t-tests
This is where you are only testing one sample, for example the number of owls in an area over the past 10 years. Usually you would compare your data with a known value, typically a mean that has been derived from previous research. You want to test the null hypothesis, i.e. is the mean of the sample the same as the known mean? A one-sample t-test is used to compare a sample mean $\bar{x}-$ (calculated using the data) to a known ‘’population’’ mean $\mu$ (typically obtained in previous research). We want to test the null hypothesis that the population mean is equal to the sample mean. For example, we might want to test whether the proportion of red squirrels to grey squirrels in Newcastle is different from the known UK average.
The Method
As you progress through your university career you will be introduced to statistical packages such as R and Minitab that can perform these tests for you and present the final significance level. However, you may also be introduced to how to conduct and interpret hypothesis test without using such software (this is good to demonstrate a thorough knowledge of what is really happening with the data). This is done as follows:
- We must first identify the null and alternative hypothesis.
- Now we calculate the test statistic using the formula below.
\begin{equation} t = \dfrac{\bar{x}-\mu}{\sqrt{\dfrac{s^2}{n}}} \end{equation}
Where $\bar{x}-$ is the sample mean, $\mu$ is the population mean, $n$ is our sample size and $s$ is the sample standard deviation.
- Now you use t-tables (see below) to find the $10$%, $5$% and $1$% critical values at the correct degrees of freedom ($n-1$) and compare our t-statistic to the appropriate critical value.
- Make conclusions. If your t-statistic is greater than any of these values we have a significant result at that level, meaning you can reject the null hypothesis, and if not accept it.
Worked Example 2
Worked Example - One Sample t-test

The number of owls in an area has been recorded for the past 50 years and the average number for these past 50 years (in a previous experiment) was found to be $106$. Over the last 9 years the counts have been recorded in the table below.
Has there been a change in the number of owls in the area?
|
Year |
Owl Count |
|---|---|
|
2005 |
108 |
|
2006 |
131 |
|
2007 |
156 |
|
2008 |
113 |
|
2009 |
105 |
|
2010 |
99 |
|
2011 |
140 |
|
2012 |
123 |
|
2013 |
110 |
Solution
For the last 9 years, the mean number of owls has been $120.6$ (1 d.p.) with a standard deviation of $18.6$.
The null hypothesis is that the number of owls has remained the same for the past 50 years. The hypothesis is that the number of owls has changed (from $106$). (Note: This is a two tailed t-test because we are just testing for a change, with no specific direction.) I.e.
- $H_0$: The number of owls has not changed.
- $H_1$: The number of owls has changed.
Using Minitab and R we find the t statistic is $2.342$ (3 d.p.). $n = 9$, so we will compare our t statistic to a t table on $9 - 1 = 8$ degrees of freedom.

|centre
Looking at the table, we can see that the critical t-value at the $95$% level $(P=0.05)$ is $2.306$. We see that $2.342$ is greater than $2.306$. Therefore, our t-statistic is statistically significant at the $95$% level and its corresponding P-value will be less than $0.05$.
We have evidence for the hypothesis and thus can conclude that the number of owls has changed.
Here are video tutorials on using R Studio and Minitab (ver. 16) for this example:
Two Sample t-tests
A two sample t-test compares two samples of normally distributed data where the population variance is unknown and the sample sizes are small ($n \lt 30$). We shall look at two types of two sample t-tests:
- Paired t-test/related t-test - comparing two sets of results which are linked (where you test the same group of participants twice or your two groups are similar). See worked example later.
- Independent/unrelated t-test - there is no link between the groups (different independent groups).
The main difference between these two tests is that the t statistic is calculated differently (using differences for Paired), however Minitab and R calculate this for you, once you specify which type of two sample t-test you would like to perform.
See the page of worked examples.
We use F-tests (usually in Minitab or R) to check our two samples have equal variances. See F-test for more information. Minitab and R also can be used to test for normality.
The t-table
Here is an example of a t-table with explanations of what each bit means. (This is for a two tailed or paired t-test, for a one-tailed t-test the probabilities are halved-see worked example below). 
Worked Example 3
Worked Example - Two Sample Paired t-test
This example is very similar to examples in the lecture notes in the first year animal behaviour module (ACE1027).
This is a paired t-test because there is one group being tested twice, rather than two independent groups.
A class were conducting an experiment to assess interobserver reliability. They observed stabled horses performing stereotypes (repetitive behaviours indicative of poor welfare: weaving, wind sucking and crib biting). They watched the footage 3 times. They assessed whether their observation and recording skills had improved each time they watched. They used data from a group of animal behaviourist students and performed intra-observation agreement calculations between watching the first and second time, then between the second and third times. The groups results are displayed in the table below.
The results were $44$% agreement between the first two observations and $61$% on the second. This seemed like a difference. They conducted a t-test and found the t statistic to be $1.731$ with $P = 0.134$. Is this a significant result?
|
First to Second |
Second to Third |
|---|---|
|
16 |
41 |
|
41 |
54 |
|
65 |
76 |
|
65 |
61 |
|
12 |
83 |
|
45 |
46 |
|
68 |
69 |
Solution

|centre
Since the t statistic $1.731$ is less than the t value of $2.447$ on $6$ degrees of freedom at $95$% level $(P = 0.05)$ (circled in the table above), we conclude that this is not statistically significant. There is no change.
The P value is $0.134$, which is approaching a trend, suggesting more experiments are needed to be more conclusive.
Worked Example 4
Worked Example - Two Sample Independent t-test
A behaviourist is interested in time taken to complete a maze for two different strains of laboratory rat. The trial involves 20 animals, 10 rats were from a strain selected according to the performance of their parents and 10 rats were from an unselected line. The time in seconds to complete the maze is recorded in the table below.
Is there a difference between the average times to complete the maze for the two strains?
|
Selected Strain |
Unselected Strain |
|---|---|
|
30 |
35 |
|
52 |
40 |
|
37 |
59 |
|
49 |
29 |
|
27 |
60 |
35 |
35 |
|
52 |
65 |
|
40 |
49 |
|
43 |
73 |
|
61 |
39 |
Solution
The mean for the selected strain is $42.6$ and the standard deviation is $10.8$. The mean for the unselected strain is $48.4$ and the standard deviation is $15.0$.
- $H_0$: There is no difference between the two strains.
- $H_1$: There is a difference between the two strains.
- Note: This is a two tailed t-test.
Using Minitab we find the t-statistic is $0.99$. (R calculates it as $0.992$.) We compare this to the t-value on $n_1 + n_2 - 2 = 18$ degrees of freedom.

|centre
Looking at the table, we can see that the critical t-value at the $95$% level $(P=0.05)$ is $2.101$. We see that $0.992$ is less than $2.101$ so our t-statistic is not significant at the $95$% level. Minitab calculates $P = 0.336$, which means there is no evidence to accept the hypothesis.
There is no difference in average time to complete the maze between the two strains.
Here are video tutorials for Minitab (ver. 16) and R Studio for this example:
Test Yourself
Try our Numbas test on hypothesis testing: Practising confidence intervals and hypothesis tests
t or z-test??
Often it can be difficult to decide whether to use a $z$-test or a t-test as they are both very similar. Here are some tips to help you decide:
- If you have a sample which is large (a good guide is $n \geq 30$), then you can use a $z$-test.
- If the population variance $(\sigma^2)$ is known, then we use a $z$ test.
- If the population variance ($\sigma^2$) is unknown and the sample is large ($n \geq 30$) then we use a $z$-test. In the test statistic, we replace the population variance $\sigma^2$ with $s^2$.
- If the population variance ($\sigma^2$) is unknown and we have a small ($n \lt 30$) sample then we use a t-test.
- If your data is not independent (for instance re-testing the same group) then you use a paired test.
The following diagram can be used to help you decide which test is appropriate too.
 (For more information about each test click the boxes.)
(For more information about each test click the boxes.)
- When using two sample tests, you need to make sure the population variances are equal.
- If your data is in the form of frequencies then you use a Chi-Square test.
Test Yourself
Try our Numbas test on hypothesis testing: Hypothesis testing and confidence intervals and also two-sample tests.
See Also
For more information about the topics covered here see the introduction to hypothesis testing.