Simultaneous Linear Equations (Business)
Simultaneous Linear Equations
Linear equations are widely used for modelling. Sometimes you will be asked to find the values of two variables (unknowns) by solving two equations at the same time. These types of equations are called simultaneous equations.
Suppose that the demand for a good is modelled as $Q = -\frac{1}{2}P+120$ and the supply is $Q = 2P +30$. The market is in equilibrium at the values of $P$ and $Q$ which make both of these equations true. These particular values of $P$ and $Q$ are the solution to this pair of equations. Since the solution to the pair of equations is at the values of $P$ and $Q$ for which both equations are true, it must lie on both straight lines. Therefore, it must be the point where the two lines intersect.
The following worked example will demonstrate how to solve a pair of simultaneous linear equations.
Worked Example
Worked Example - Simultaneous Linear Equations
Consider the following two equations.
\begin{align} 4y &= 2x + 7 \; \; \; \; \; \; \; \; &\color{purple}{(\star)}\\ 2y &= -10x+20 \; \; &\color{purple}{(\dagger)}\\ \end{align}.
They are labelled $\color{purple}{(\star)}$ and $\color{purple}{(\dagger)}$ for convenience.
Find the point of intersection.
Solution
First rearrange the equations to make them easier to work with.
\begin{align} 4y -2x &= 7 &\color{purple}{(\star)}\\ 2y +10x &= 20 &\color{purple}{(\dagger)}\\ \end{align}
To find the point of intersection, you multiply one of the equations by a number. This number is chosen so that one of the following is true:
A. a term (e.g. $10x$) appears in both equations.
OR
B. a term is positive in one of the equations (e.g. $10x$) and negative ($-10x$) in the other.
So, if you multiply $\color{purple}{(\star)}$ by $5$, we then have:
\begin{align} 20y -10x &= 35 &\color{purple}{(\star \star)}\\ 2y +10x &= 20. &\color{purple}{(\dagger \dagger)}\\ \end{align}
Here, one equation contains $-10x$ and the other has $10x$, (case B). (Note: Here, $\color{purple}{(\dagger \dagger)}$ is the same as $\color{purple}{(\dagger)}$.)
On the other hand, you could multiply $\color{purple}{(\dagger)}$ by $2$, which would result in:
\begin{align} 4y -2x &= 7 &\color{purple}{(\star \star \star)}\\ 4y +20x &= 40. &\color{purple}{(\dagger \dagger \dagger)}\\ \end{align}
Here both equations contain the term $4y$, (case A). (Note: $\color{purple}{(\star \star \star)}$ is the same as $\color{purple}{(\star)}$ here.)
For case A, we subtract one equation from the other, term by term:
\begin{align} &4y -2x=7\\ &4y +20x= 40\\ &\overline{\quad\;\, -22x=-33} \end{align}
We can now solve $-22x=-33$ by dividing both sides by $-22$ to get $x = \dfrac{3}{2}$. Now substitute our solution for $x$ into either of $\color{purple}{(\dagger)}$ or $\color{purple}{(\star)}$ to find $y$. Substituting $x=\dfrac{3}{2}$ into $\color{purple}{(\star)}$ gives us:
\begin{align} 4y -3 &= 7\\ 4y & = 10\\ y &= \dfrac{10}{4}\\ &=\dfrac{5}{2} \end{align}
Therefore, the solution to the pair of original equations is $x=\dfrac{3}{2}, y = \dfrac{5}{2}$ or the point $\left(\dfrac{3}{2},\dfrac{5}{2}\right)$.
For case B, you must add the two equations together:
\begin{align} &20y -10x = 35\\ &2y +10x = 20\\ &\overline{22y\quad\;\,=55} \end{align}
We can now solve $22y=55$ for $y$ by dividing both sides by $22$. This gives $y= \dfrac{55}{22}=\dfrac{5}{2}$. Substituting this value of $y$ into either of $\color{purple}{(\dagger)}$ or $\color{purple}{(\star)}$ will enable us to find a solution for $x$. This time we shall use $\color{purple}{(\dagger \dagger)}$, to give us,
\begin{align} 5 +10x &= 20. &\color{purple}{(\dagger \dagger)}\\ 10x &= 15\\ x &= \dfrac{15}{10}\\ &= \dfrac{3}{2}.\\ \end{align}
The solution is then the point $\left(\dfrac{3}{2},\dfrac{5}{2}\right)$ or $x = \dfrac{3}{2}, y = \dfrac{5}{2}.$
Both cases produce the same solution. The intersection point is $\left(\dfrac{3}{2},\dfrac{5}{2}\right)$.
Here is a graphical solution for this example.
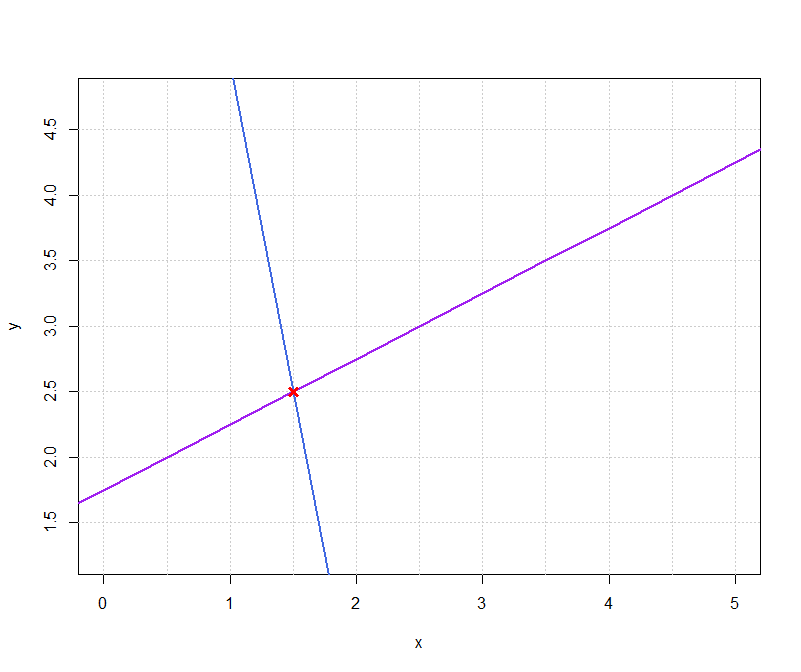
For this particular example, finding the point of intersection graphically is not too difficult. However, what if we wish to solve.
\begin{align} 17y - 3x &= 8\\ \text{and}\\ 9y +16x &= 13?\\ \end{align}
The graph looks like this:
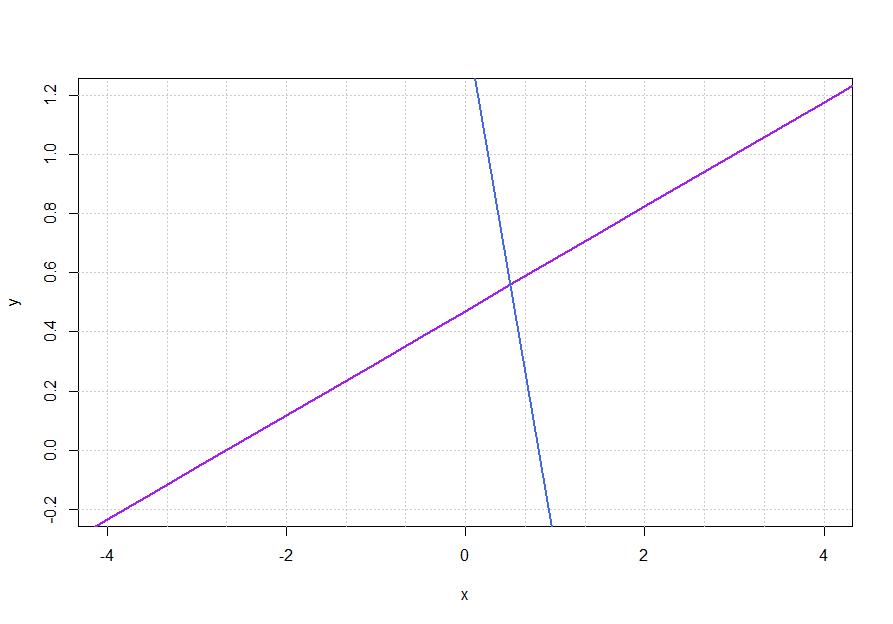
As you can see, finding the intersection point graphically is not as straightforward as above and could result in a lack of precision. This demonstrates how it is important to know how to solve paired linear equations using the above method, rather than using graphs.
No Solutions and Infinite Solutions
In the examples above, there is exactly one solution $x,y$. For most cases this will be true. However, we must be also wary of two other possibilities.
Consider:
\begin{align} 3x - 4y &= 12\\ -9x+12y &= 5.\\ \end{align}
Solving in the way described above we would multiply the first equation $3x - 4y= 12$ by $3$ to give $9x-12y=36$. There is a $-12y$ in this equation and a $12y$ in the second equation (case B). To solve this set of equations, we must therefore begin by adding these 2 equations together as follows:
\begin{align} &9x - 12y= 36\\ &-9x+12y= 5\\ &\overline{0x + 0y= 41} \end{align}
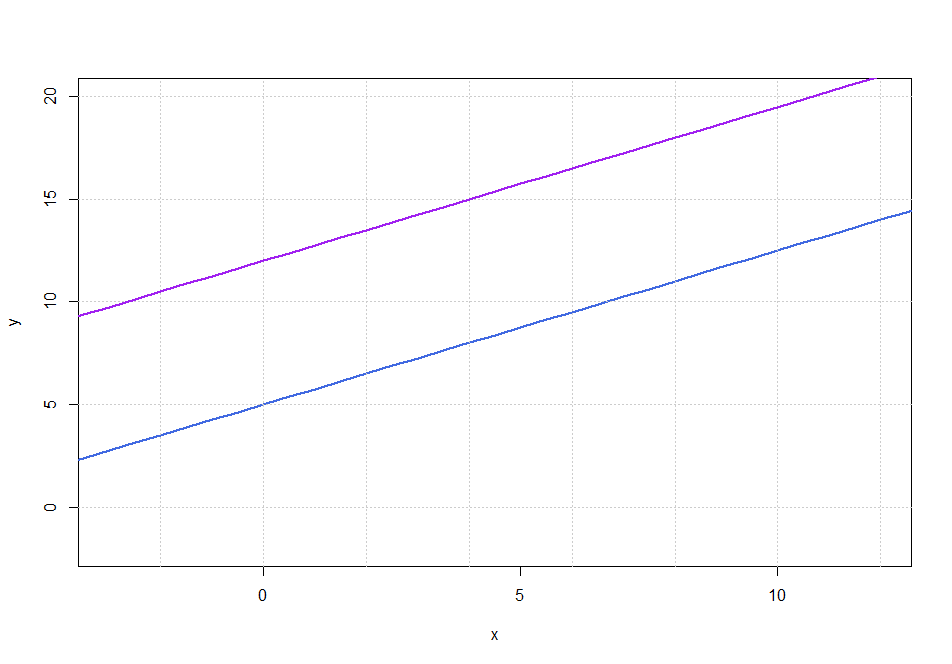
Since $0x + 0y$ is zero for all values of $x$ and $y$, this equation is claiming that $0 = 41$, which is false. This informs us that there is no solution to the pair of equations. The graph below demonstrates why there is no solution. You can see that the lines are parallel so they never intersect.
Now consider the following pair of equations:
\begin{align} 2y + 2x = 5\\ 4y + 4x = 10 \end{align}
To solve these we would multiply the first equation by $2$ to get $4y+4x = 10$ and subtract this equation from the second equation (or equivalently, subtract the second equation from this equation) to get:
\begin{align} &4y + 4x = 10\\ &4y + 4x = 10\\ &\overline{0x + 0y= 0}\\ \end{align}
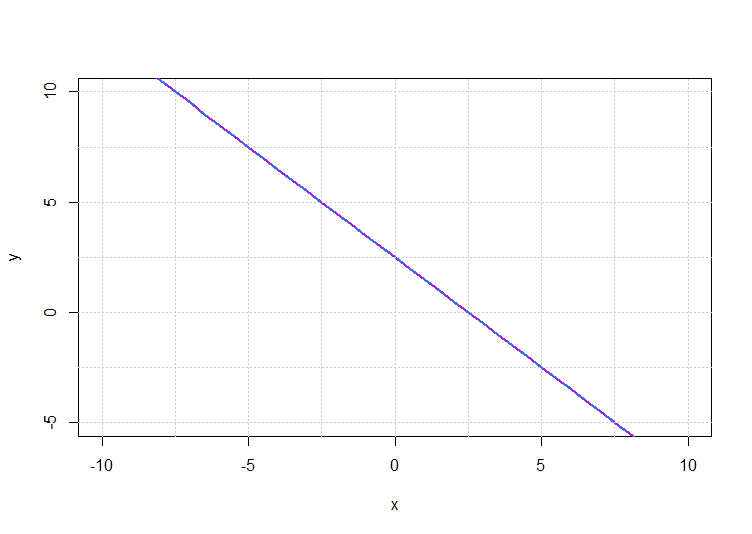
The equation $0x + 0y = 0$ is valid for any values of $x$ and $y$. Therefore, there are an infinite number of solutions. The graph below shows the two lines corresponding to the given equations. As you can see they are in fact both the same line, which is why there are an infinite number of solutions (they “intersect” for all values of $x$ and $y$).
|center
Test Yourself
Try our Numbas test on linear programming
See Also
For developing the techniques seen in this section see Functions and Rates of Change.