Sets and Venn Diagrams (Economics)
Set Theory
Set theory is the branch of mathematics which studies sets.
A set is a collection of elements (or objects) and can be considered as an element itself. We often denote a set using a capital letter. Sets are used to group and describe elements which share a similar property. If an element $x$ is included in a set we say that $x$ is a member of that set. Sets are called disjoint if they have none of the same elements.
The sample space (or universal set) is a set which includes all elements that a set may contain. It is typically denoted using the letter $S$. If we have only one set $A$, then the sample space is the same as that set: $S=A$.
The empty (or null) set $\varnothing$ contains no elements at all.
Defining a Set
There are $2$ main ways in which we can define a set. These are known as the listing (or roster) method and the rule method.
Listing Method
This method involves writing the members of a set as a list, separated by commas and enclosed within curly braces. For example, the four seasons are a set and could be written as {Summer, Autumn, Spring, Winter}.
Note: The order of the elements in the list doesn’t matter. For example, we could have written the set of seasons as {Spring, Autumn, Summer, Winter} or {Winter, Autumn, Spring, Summer}.
Rule Method
This method involves specifying a rule or condition which can be used to decide whether an object can belong to the set. This rule is written inside a pair of curly braces and can be written either as a statement or expressed symbolically or written using a combination of statements and symbols.
The rule method is often preferred when defining larger sets where it would be difficult or time consuming to list all of the elements in a set.
For example, a set $A$ whose elements included all the positive integers could be defined symbolically as: \[A=\{x|x\gt0\}\] or in statement form as: \[A=\{x|x \text{ is a positive number}\}\] The set $B$, whose elements include all the natural numbers from $1$ to $25$ inclusive could be defined symbolically as: \[B=\{x|x \in \mathbb{N},1\leq x \leq 25\}\] or using a statement and symbols as: \[B=\{x|x \text{ is a natural number}, 1\leq x \leq 25\}\]
Types of Sets
Finite Sets
Finite sets are sets which contain a limited and countable number of elements. The sets $A=\{1,2,6\}$ and $B=\{x|1\leq x \leq 10\}$ are both examples of finite sets.
Infinite Sets
Infinite sets contain an unlimited (or infinite) and uncountable number of elements. For example, the sets $C=\{2, 4, 6, ...\}$ and $D=\{x|x\leq 0\}$ are both infinite sets.
Venn diagrams
Venn diagrams are a useful way of visualizing relationships between sets.
When we draw Venn diagrams, sets are represented by circles. The inside of a circle represents all the elements that are members of that set and the outside of the circle represents all elements which are not members of that set.
The areas where circles overlap represents the set of elements which are in all of the sets corresponding to the overlapping circles. We call this area the intersection of the (overlapping) sets.
The sample space is represented by a rectangle which is drawn around all of the circles and we write the set name of the sample space (typically the letter $S$) in the left-hand corner. If we want to partition the sample set into multiple parts, we draw lines to divide the rectangle into the required number of parts.
Worked Example
In an Economics seminar group there are $32$ students. $19$ of these students say they enjoy studying Microeconomics, $17$ say they enjoy studying Macroeconomics, and $5$ say that they enjoy studying neither Microeconomics nor Macroeconomics. How many of the students in the seminar group enjoy studying both Microeconomics and Macroeconomics?
Solution
We can solve this problem by drawing a Venn diagram to represent the situation and adding each new piece of information to the diagram as we go.
The sample space is the set of all $32$ students in the seminar group. We will denote the sample space by the letter $S$.
Denote the set of ($19$) students who enjoy studying Microeconomics by $I$ and the set of ($17$) students who enjoy studying Macroeconomics by $A$. These sets are represented by circles. We want to known how many students there are in the intersection of these two circles (who enjoy studying both subjects).
The $5$ students who enjoy neither of the subjects go on the outside of the circles. We know the total in the Microeconomics circle needs to be $19$ but we can't put this in the circle because we don't know how many should go in the intersection and how many should go in the right hand part of the Microeconomics circle (those who enjoy studying only Microeconomics). We have the same problem for the Macroeconomics circle so our Venn diagram currently looks like this:
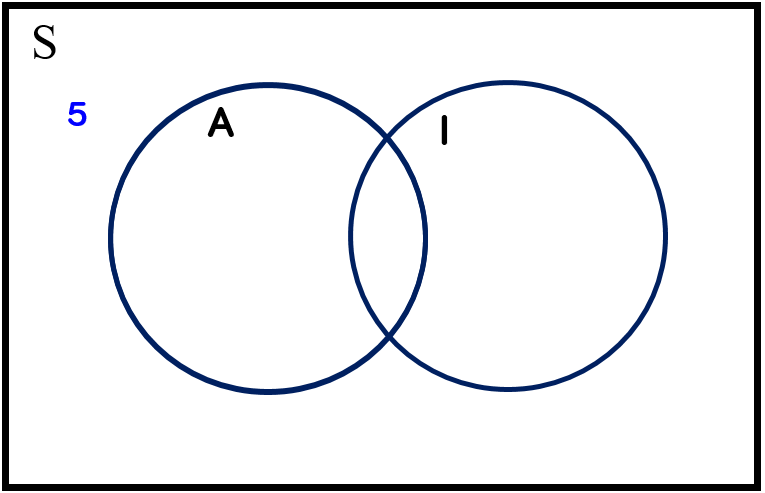
We know there are $32$ students in the group, and if there are $5$ students outside the circles then the other three sections must add up to $27$. We know there are $17$ students who enjoy Macroeconomics, so the middle and left section must add up to $17$. This leaves $10$ in the right-hand section of the $I$ circle because $27-17=10$.
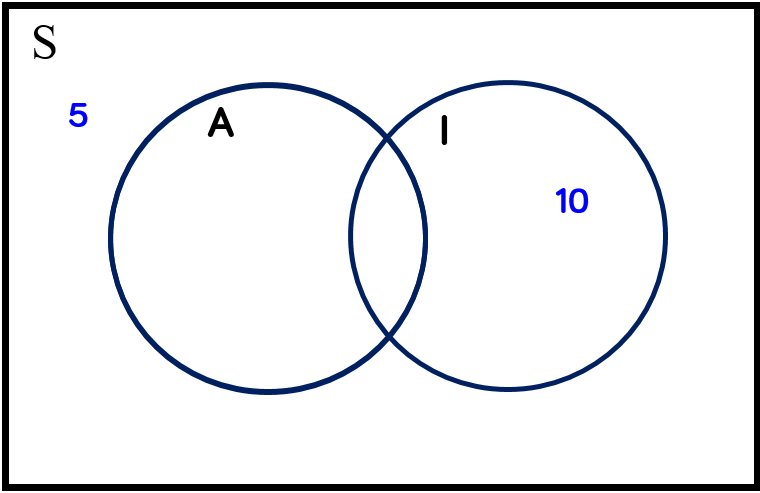
Since there are $19$ students who enjoy Microeconomics, the two parts of the Microeconomics circle should add up to $19$ so we can now find the number in the intersection by subtracting $10$ from $19$: $19–10=9$.
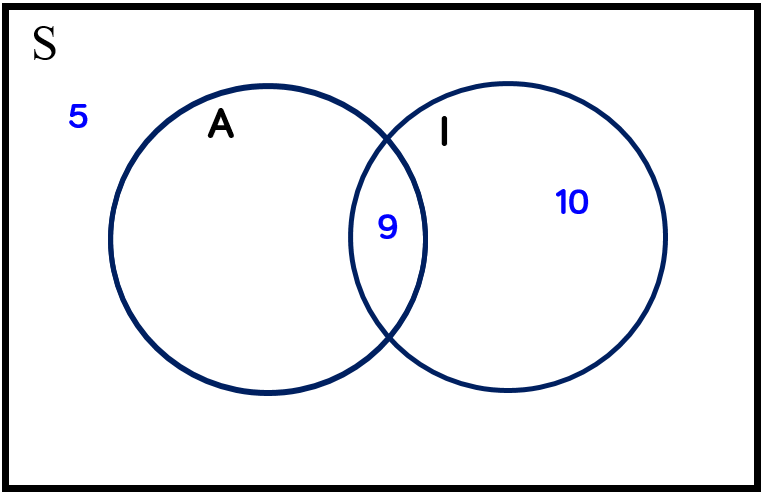
There are $19$ students who enjoy Microeconomics, and $27-19=8$, so the number who enjoy Macroeconomics but not enjoy Macroeconomics must be $8$.
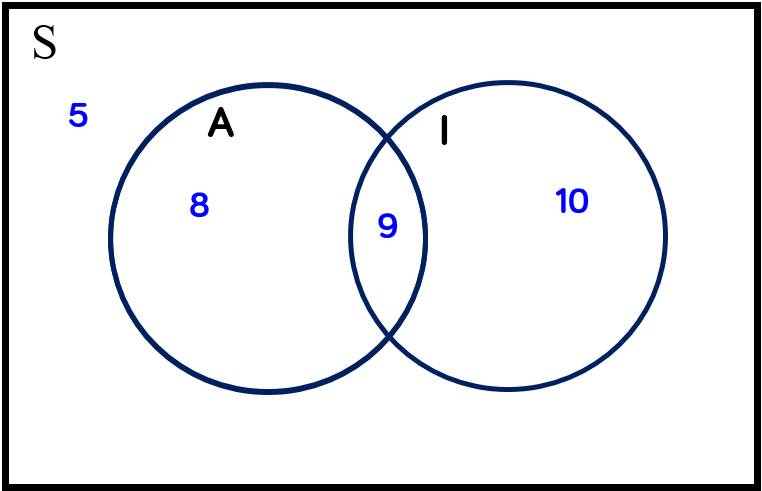
If we check all four facts we were given, we can now see they are all true. In particular, there are $32$ students in the seminar group and $32$ in the venn diagram.
There are $9$ students who enjoy both Microeconomics and Macroeconomics.
Set Notation
Suppose that our sample space is the set of natural numbers $\mathbb{N}=\{1, 2, 3, 4, ...\}$. Let $A$ be the set containing the numbers $1$ to $5$ (inclusive), $B$ be the set containing the numbers $1$ to $3$ (inclusive) and $C$ be the set containing the numbers $1$, $2$ and $6$; that is we have $A=\{1, 2, 3, 4, 5\}$, $B=\{1, 2, 3\}$ and $C=\{1, 2, 6\}$. We can represent the following relationships as follows:
Symbol |
Pronounciation |
Interpretation |
Set |
Venn Diagram |
|---|---|---|---|---|
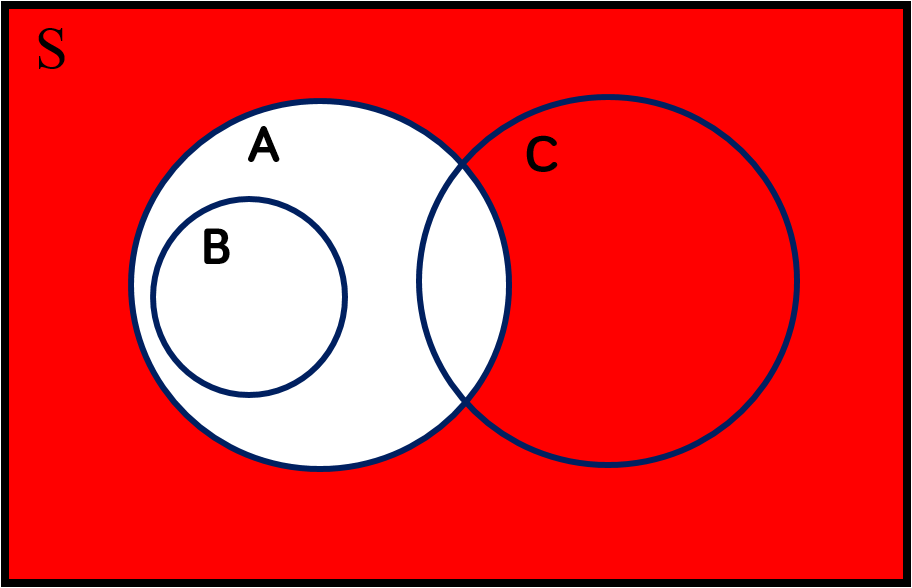
$A^c$ |
$A$ complement |
Every element which is not a member of $A$ |
$\{6, 7, 8,...\}$ |
|
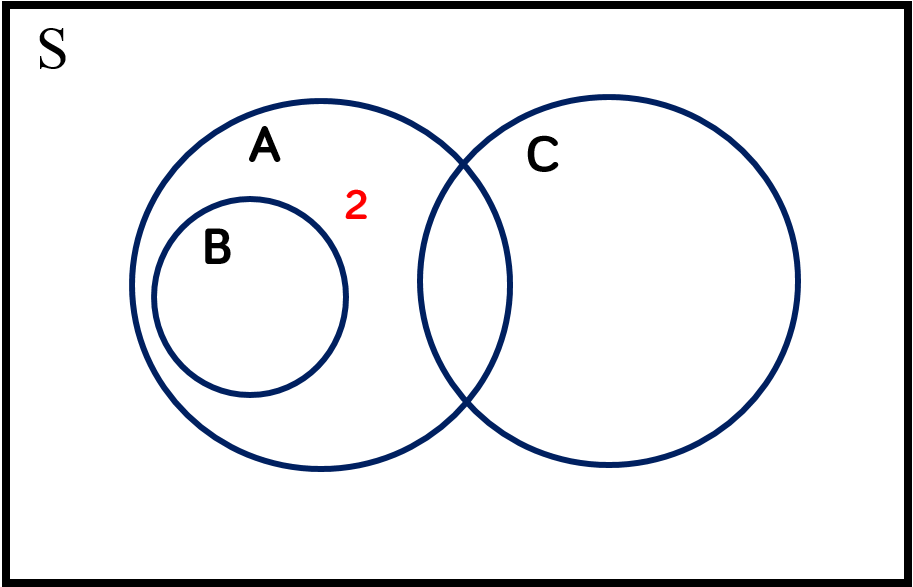
$2 \in A$ |
$2$ is an element of $A$ |
The number $2$ is a member of the set $A$ |
|
|
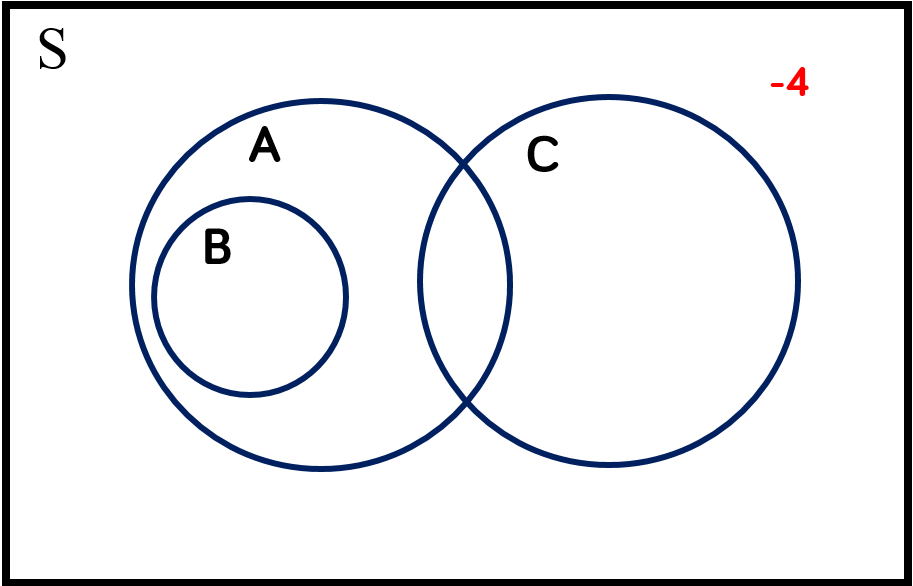
$-4 \notin C$ |
$-4$ is not an element of $C$ |
The number $-4$ is not a member of the set $C$ |
|
|
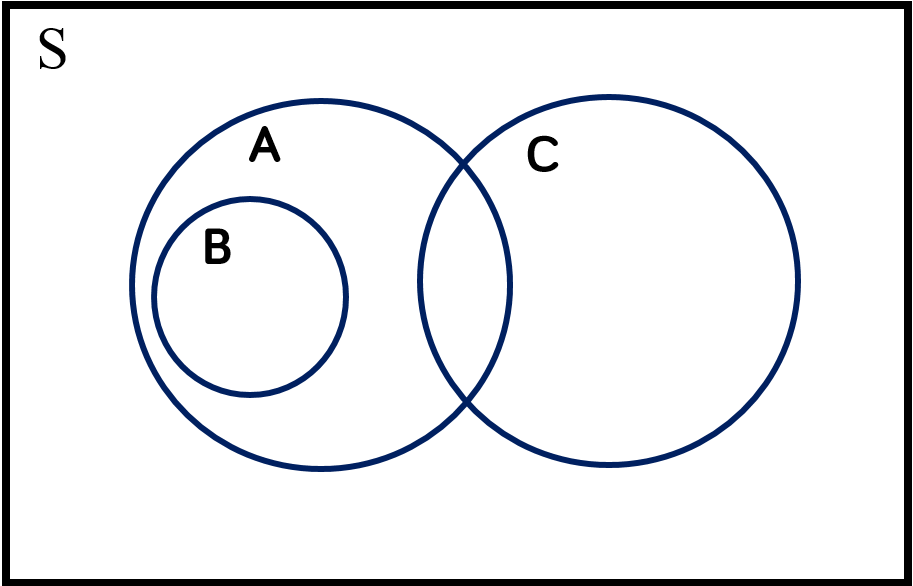
$A \supset B$ |
$A$ contains $B$ |
Every element of $B$ is also an element of $A$ |
|
|
$B \subset A$ |
$B$ is a subset of $A$ |
Every element of $B$ is also an element of $A$ |

|
|
$A \cup C$ |
$A$ union $C$ |
Every element which is a member of $A$ OR $C$ |
$\{1, 2, 3, 4, 5, 6\}$ |

|
$A \cap C$ |
$A$ intersect $C$ |
Every element which is a member of both $A$ AND $C$ |
$\{1, 2\}$ |
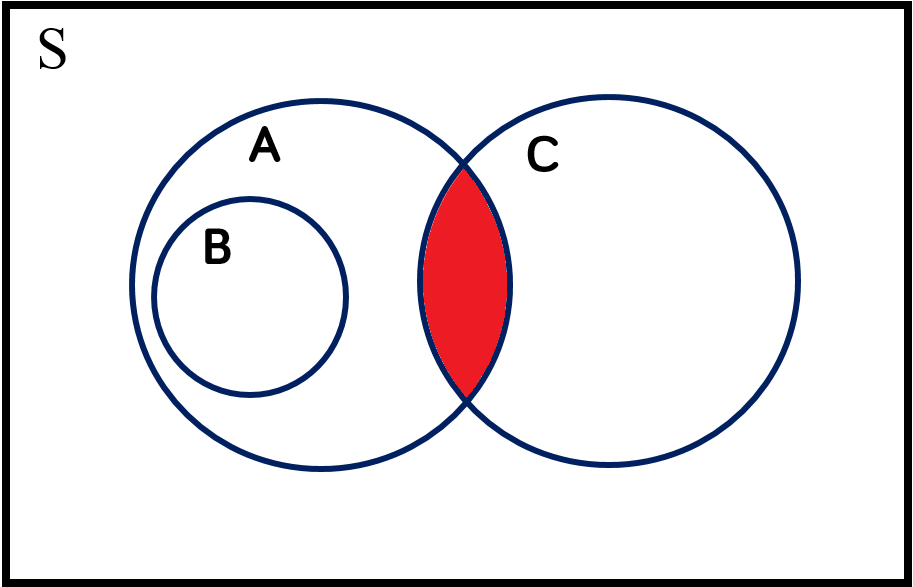
|
Laws of Operations on Sets
The laws of operations on sets are very similar to the fundamental laws of algebra, with the operations addition and multiplication replaced by union and intersection.
Necessity and Sufficiency Applied to Sets
We can use the concepts of necessary and sufficient conditions to describe relationships between sets.
For example, the set of natural numbers $\mathbb{N}$ is a subset of the set of real numbers $\mathbb{R}$, since every natural number is a real number. In other words, being in the set $\mathbb{N}$ is a sufficient but not a necessary condition for being in the set $\mathbb{R}$. We can write this as: \[\mathbb{N} \Rightarrow \mathbb{R}.\]
Another way to think about the relationship between the sets $\mathbb{R}$ and $\mathbb{N}$ is that being in the set $\mathbb{R}$ is a necessary but not a sufficient condition for being in the set $\mathbb{N}$. For example, $3.5$ is a real number but not a natural number. We thus have \[\mathbb{R} \Leftarrow \mathbb{N}.\]
Note: In set notation we would write the relationship between these two sets as $\mathbb{N} \subset \mathbb{R}$ or $\mathbb{R} \supset \mathbb{N}$.
Example
Consider again the sets $A=\{1, 2, 3, 4, 5\}$, $B=\{1, 2, 3\}$ and $C=\{1, 2, 6\}$ from above. Consider also the set $D=\{1, 2, 6\}$. Describe the relationships between the following pairs of sets in terms of necessity and sufficiency:
1) $A$ and $B$
2) $C$ and $D$
Solution
1) We have already observed that the set $B$ is a subset of $A$. We can write this relationship as either
\[B \Rightarrow A \text{ or } A \Leftarrow B.\]
which says “being in the set $B$ is a sufficient condition for being in the set $A$”.
2) $C$ and $D$ contain exactly the same elements: they are the same set. Being in the set $C$ is thus both a necessary and a sufficient condition for being in the set $D$ (and vice versa) and we can write:
\[C \Leftrightarrow D.\]