Histograms

Definition

A histogram is a graphical representation of discrete or continuous data. The area of a bar in a histogram is equal to the frequency. The $y$-axis is plotted by frequency density (which is proportional to the frequency) and the $x$-axis is plotted with the range of values divided into intervals.

A histogram can only be used to plot numerical values and it is usually used for large data sets. It is useful for detecting outliers and/or gaps in the data set.

Worked Example

Worked Example

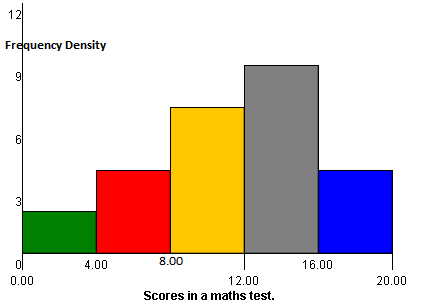
Construct a histogram of the following marks in a maths test where the maximum possible mark is 20. \[2,\ 4,\ 14,\ 14,\ 16,\ 17,\ 13,\ 16,\ 7,\] \[8,\ 9,\ 10,\ 11,\ 19,\ 18,\ 15,\ 15,\ 16,\] \[13,\ 12,\ 7,\ 8,\ 9,\ 12,\ 11,\ 18.\]

Solution

Firstly order your data so it will make it easier to group.

\[2,\ 4,\ 7,\ 7,\ 8,\ 8,\ 9,\ 9,\ 10,\ 11,\] \[11,\ 12,\ 12,\ 13,\ 13,\ 14,\ 14,\ 15,\ 15,\ 16,\] \[16,\ 16,\ 17,\ 18,\ 18,\ 19.\]

Next, look at your data and find the minimum and maximum values and choose a sensible class width. The minimum value is $2$ and the maximum value is $19$, a sensible class width would be anywhere between $3$ and $5$; for this example you might choose $4$. Your class intervals will be $0-4$, $5-8$, $9-12$, $13-16$ and $17-20$.

Now you need to collect your data into a frequency distribution table.

Test Score

Frequency

$0-4$

$2$

$5-8$

$4$

$9-12$

$7$

$13-16$

$9$

$17-20$

$4$

This can now be plotted on a histogram.

|250px

|250px

Video Example

This is Khan Academy's video on creating a histogram.

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

Test Yourself

External Resources