One-tailed and Two-tailed Tests
Definition
A one-tailed test results from an alternative hypothesis which specifies a direction. i.e. when the alternative hypothesis states that the parameter is in fact either bigger or smaller than the value specified in the null hypothesis.
A two-tailed test results from an alternative hypothesis which does not specify a direction. i.e. when the alternative hypothesis states that the null hypothesis is wrong.
One-tailed Tests
A one-tailed test may be either left-tailed or right-tailed.
A left-tailed test is used when the alternative hypothesis states that the true value of the parameter specified in the null hypothesis is less than the null hypothesis claims.
A right-tailed test is used when the alternative hypothesis states that the true value of the parameter specified in the null hypothesis is greater than the null hypothesis claims
Two-tailed Tests
The main difference between one-tailed and two-tailed tests is that one-tailed tests will only have one critical region whereas two-tailed tests will have two critical regions. If we require a $100(1-\alpha)$% confidence interval we have to make some adjustments when using a two-tailed test.
The confidence interval must remain a constant size, so if we are performing a two-tailed test, as there are twice as many critical regions then these critical regions must be half the size. This means that when we read the tables, when performing a two-tailed test, we need to consider $\frac{\alpha}{2}$ rather than $\alpha$.
Worked Example 1
Worked Example
A light bulb manufacturer claims that its' energy saving light bulbs last an average of 60 days. Set up a hypothesis test to check this claim and comment on what sort of test we need to use.
Solution
So we have
- $H_0$ : The mean lifetime of an energy-saving light bulb is $60$ days.
- $H_1$ : The mean lifetime of an energy-saving light bulb is not $60$ days.
Because of the “is not” in the alternative hypothesis, we have to consider both the possibility that the lifetime of the energy-saving light bulb is greater than $60$ and that it is less than $60$. This means we have to use a two-tailed test.
Worked Example 2
Worked Example
The manufacturer now decides that it is only interested whether the mean lifetime of an energy-saving light bulb is less than 60 days. What changes would you make from Example 1?
Solution
So we have
- $H_0$ : The mean lifetime of an energy-saving light bulb is $60$ days.
- $H_1$ : The mean lifetime of an energy-saving light bulb is less than $60$ days.
Now we have a “less than” in the alternative hypothesis. This means that instead of performing a two-tailed test, we will perform a left-sided one-tailed test.
Worked Example 3
Worked Example
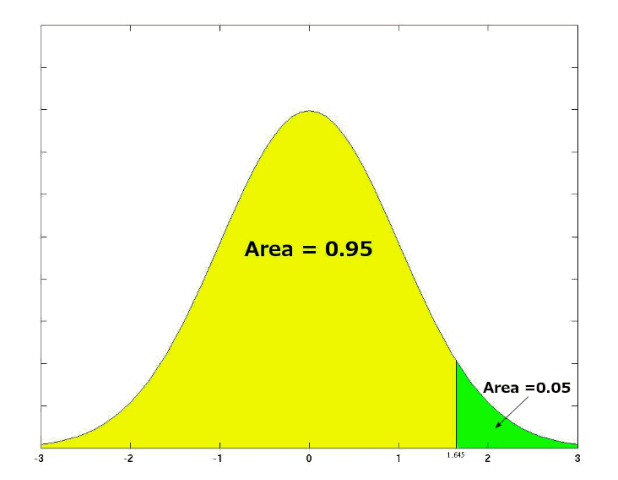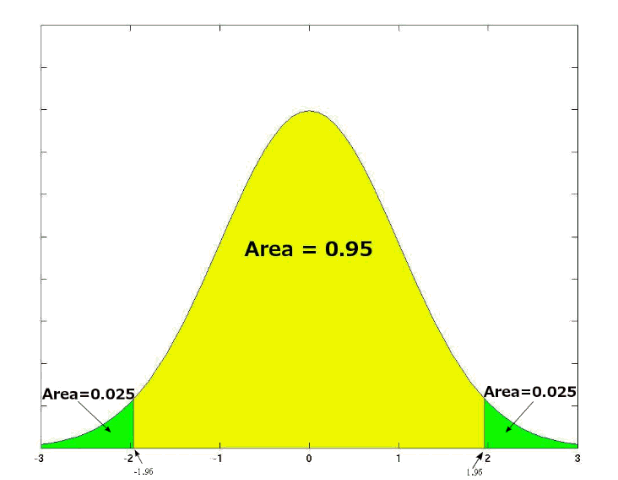
Find the critical values of the normal distribution using a $5$% significance level for both a one-tailed and a two-tailed test.
Solution
For the (right-sided) one-tailed test with a $5$% significance level, $z_{1-\alpha}=1.645$. (A left-tailed test would result in the critical value of $-1.645$.) For the two tailed test, $z_{1-\frac{\alpha}{2} } = 1.96$. The values are obtained from the tables of the inverse of the cumulative distribution function of the normal distribution.