Derivatives and Differentiation (Economics)

The Slope of a Curve

We have already seen that the slope of a straight line can be measured by dividing the change in the value of $y$ between any two points on the line by the corresponding change in the value of $x$ between the same two points: \[\text{Slope of a straight line }=\dfrac{y_1 - y_0}{x_1 - x_0}=\frac{\triangle y}{\triangle x}\]

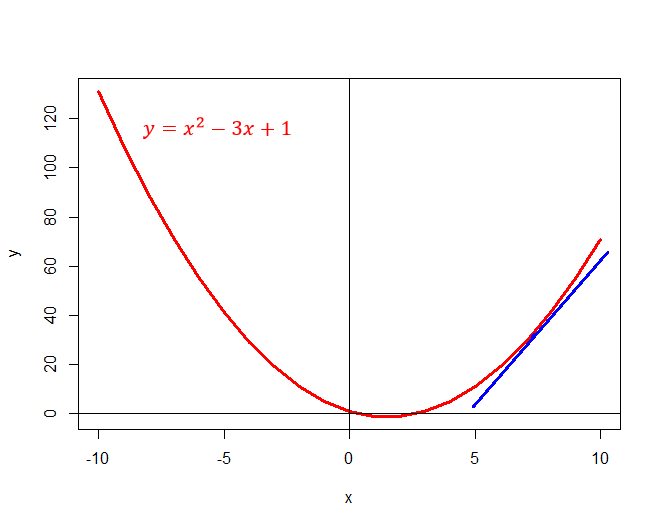
For a curve, measuring the slope is more difficult because the slope changes as we move along the curve. For example, in the plot below we can see that the slope of the quadratic function $y=x^2-3x+1$ becomes steeper as we move away from the point where $x=1.5$ and $y=-1.25$.

A tangent to a curve is defined as a straight line which touches the curve at a single point. We can overcome the problem of measuring the slope of a curve by noticing that the slope of a curve is equal to the slope of the tangent to curve $\frac{\triangle y}{\triangle x}$ at the point where they touch. The slope of the tangent to a curve at this point is known as the derivative of the function with respect to $x$ and is denoted by: \[\dfrac{\mathrm{d} y}{\mathrm{d} x}\] which is pronounced as “dee y by dee x”. This is the rate at which the output of a function $y$ changes when we change the input by a very small amount.

Finding the derivative of a curve is known as differentiation.

But how can we measure the slope of the tangent at any point on the curve?

A chord is a straight line connecting two points on a curve. The slope of a chord is equal to the average slope of the curve between the two points. For example, in the plot below we have added a chord to the graph of $y=x^2-3x+1$ between the points ($x_0, y_0$) and ($x_1, y_1$). The slope of this chord is equal to \[\dfrac{y_1 - y_0}{x_1 - x_0}=\frac{\triangle y}{\triangle x}\]

By bringing the points ($x_0, y_0$) and ($x_1, y_1$) closer and closer together ($\triangle x\rightarrow 0$), we can see that the chord will get nearer and nearer to being a tangent to the curve. In addition, the slope of the chord will become a better and better approximation to the slope of the tangent and hence, the slope of the curve. Using the notation introduced in the limits section, we have

\[\displaystyle{\lim_{\triangle x\rightarrow 0} \frac{\triangle y}{\triangle x}}=\dfrac{\mathrm{d} y}{\mathrm{d} x}\]

where $\triangle x$ is a very small change in $x$ and $\triangle y$ is a very small change in $y$.

Key Point: The gradient of a curve at a given point is defined to be the gradient of the tangent at that point. We approximate the slope of this tangent by calculating the slope of a chord between $2$ points on the curve and bringing these points closer and closer together.

Note: $\dfrac{dy}{dx}$ is not a fraction.

Note: $\dfrac{dy}{dx}$ is a function of $x$ and so should contain only $x$ terms (no $y$ terms). This means that once we have found the derivative of a function, we can find the slope at any point on its curve by substituting the value of $x$ at that point into the derivative.

Note: Another way of denoting the derivative of a function $f(x)$ is $f'(x)$.

Differentiation From First Principles

Suppose we want to differentiate the function $y=x^2-3x+1$.

Let's start by drawing a chord between two points ($x_0, y_0$) and ($x_1, y_1$) on the graph of $y=x^2-3x+1$. As we've seen, the slope of this chord gives us the average gradient of the curve $y=x^2-3x+1$ between these two points and is equal to \[\frac{\triangle y}{\triangle x}=\dfrac{y_1 - y_0}{x_1 - x_0}\] Now, in order to differentiate this function, we must first express $\frac{\triangle y}{\triangle x}=\dfrac{y_1 - y_0}{x_1 - x_0}$ solely in terms of $x_0$ and $\triangle x$.

We can rearrange $\triangle x=x_1 - x_0$ to make $x_1$ the subject: \begin{eqnarray} x_1=x_0+\triangle x\;\;\;& \color{purple}{(1)} \end{eqnarray}

Then, using the fact that $y=x^2-3x+1$, we have \begin{eqnarray} y_0={x_0}^2-3{x_0}+1\;\;\;& \color{purple}{(2)} \end{eqnarray} and \begin{eqnarray} y_1={x_1}^2-3{x_1}+1\;\;\;& \color{purple}{(3)} \end{eqnarray} Substituting $\color{purple}{(1)}$ into $\color{purple}{(3)}$ gives: \begin{eqnarray} y_1=({x_0}+\triangle x)^2-3({x_0}+\triangle x)+1\;\;\;& \color{purple}{(2)} \end{eqnarray} Using $\color{purple}{(2)}$ and $\color{purple}{(3)}$, we can now rewrite the slope of the chord as: \begin{align} \dfrac{\triangle y}{\triangle x}&=\dfrac{\left(({x_0}+\triangle x)^2-3({x_0}+\triangle x)+1\right)-({x_0}^2-3{x_0}+1)}{\triangle x}\\ &=\dfrac{\left({x_0}^2+2x(\triangle x)+({\triangle x})^2-3x_0-3(\triangle x)+1\right)-({x_0}^2-3{x_0}+1)}{\triangle x}\;&\text{(expanding brackets)}\\ &=\dfrac{v^2}$ | Quotient Rule |- | $y= e^x$ | $\dfrac{\mathrm{d} y}{\mathrm{d} x}= e^x$ | - |- | $y= e^{g(x)}$ | $\dfrac{\mathrm{d} y}{\mathrm{d} x}=g'(x) e^{g(x)}$ | - |}

The Second Derivative

The derivative of a function of sometimes referred to as the first derivative of the function. This is because it is possible to differentiate the derivative of a function. This gives us the second derivative of the function and is denoted by: \[\dfrac{\mathrm{d}^2 y}{\mathrm{d} x^2}\text{ or } f''(x)\] The second derivative of a function can be thought of as the slope of the slope and very useful for optimisation. Since the second derivative is also a function, we can take its derivative giving us the third derivative, and so on.

For example, suppose we are asked to find the second derivative of the function $f(x)=x^2+5x+2$. The graph of this function is shown below:

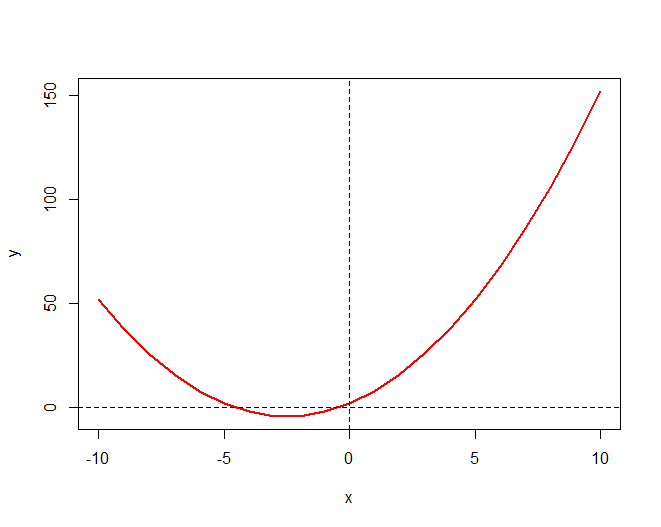
We must first find the first derivative of the function using the rules from the table above: \begin{align} f'(x)&=2\times x+5+0\\ &=2x+5 \end{align} The graph of $f'(x)=2x+5$ is shown below. Since the original function was a quadratic, its derivative is linear. As we've seen the graph of a linear function is a straight line.

To find the second derivative, we must differentiate $f'(x)=2x+5$. This gives: \[f''(x)=2\]

So the second derivative of $f(x)=x^2+5x+2$ is $f''(x)=2$.

Since the first derivative was linear, the second derivative is a constant so its graph is a straight horizontal line:

The Third Derivative

The third derivative of a function is obtained by differentiating its second derivative. It is therefore interpreted as the slope of the graph of the second derivative function, $y=f''(x)$. We denote the third derivative by: \[\dfrac{\mathrm{d}^3 y}{\mathrm{d} x^3} \text{ or } f'''(x)\]

Test Yourself

Test yourself: Numbas test on differentiation

Test yourself: Numbas test on differentiation, including the chain, product and quotient rules

External Resources