Optimisation (Economics)
Increasing and Decreasing Functions
We have seen that the derivative of a function measures the slope of the function at any point. Therefore if for a particular value of $x$:
- $\dfrac{\mathrm{d} y}{\mathrm{d} x}\gt0$ the function is positively sloped for that value of $x$
- $\dfrac{\mathrm{d} y}{\mathrm{d} x}\lt0$ the function is negatively sloped for that value of $x$
The graph of $y=x^2$ is shown below. We can see that this function has a positive slope for values of $x$ which are greater than zero and a negative slope for values of $x$ which are less than zero.
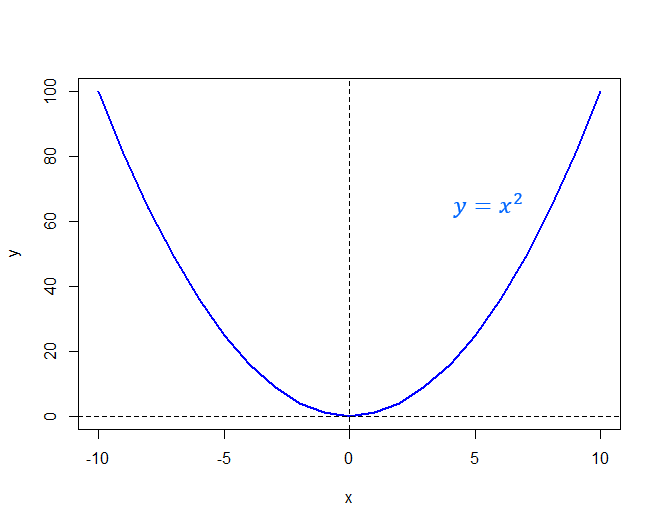
If the derivative of a function is:
- Positive for all possible values of $x$, we say the function is monotonic increasing. For example, the function $y=2x$ is monotonic increasing as all powers of $3$ are positive.
- Negative for all possible values of $x$, we say the function is monotonic decreasing. For example, the function $y=-2x$ is monotonic decreasing as all powers of $3$ so putting a minus sign in front makes all of the powers negative.


Concave and Convex
A function is said to be concave if its slope is decreasing.This means that a line drawn between any two points on the curve will never be above the graph.
A function is convex if its slope is increasing. This means that a line drawn between any two points on the curve will never be below the graph.

For example, the function $y=x^3$ is concave for all values of $x$ less than zero and convex for all values of $x$ greater than zero.

Derivatives in Action
In economics, it is often important to know when the output of a function is at its highest or lowest possible value (maximum and minimum respectively).
For example, a firm may want to know how much it needs to sell to maximize its profit function or minimize its cost function (see the worked examples below.
Finding the maximum and minimum points of a function requires differentiation and is known as optimisation. Maximum and minimum points of a function are collectively known as stationary points.
Stationary Points
A stationary point of a function is a point where the derivative of a function is equal to zero and can be a minimum, maximum, or a point of inflection. At a stationary point the slope of the graph of the function is zero (a straight line). They are called stationary points because they are points where the function is neither increasing nor decreasing.
Note:The maximum and minimum points of a function are also called turning points because the slope of the function turns from being positive to being negative.
Finding Stationary Points
We can find the stationary points of a function $f(x)$ using the following method:
1) Find the (first) derivative of the function with respect to $x$.
2) Set the derivative equal to zero \[\dfrac{\mathrm{d}f}{\mathrm{d}x}=0.\]
3) Solve the equation $\dfrac{\mathrm{d}f}{\mathrm{d}x}=0$ for $x$.This equation has one solution for each stationary point. Substituting each of these values (separately) into the function $f(x)$ will give the corresponding $y$ coordinate(s) of the stationary point(s).
4) Determine whether each stationary point is a maximum, a minimum or a point of inflection (see how to do this below).
Maximum, Minimum or Point of Inflection?
Using the Second Derivative
Once we have found the stationary points of a function we then want to know whether this point is a maximum or a minimum or a point of inflection. One way to do this is to find the second derivative by differentiating the function twice. The second derivative is denoted by
\[\frac{ \mathrm{\mathrm{d}}^2 f }{ \mathrm{\mathrm{d}}x^2 } \text{ or } f''(x).\]
Suppose that we have a stationary point at $x=a$. Then if:
- The second derivative is negative: $\dfrac{ \mathrm{d}^2 f }{ \mathrm{d}x^2 } \lt 0$ at $x=a$, we have a maximum.
- The second derivative is positive: $\dfrac{ \mathrm{d}^2 f }{ \mathrm{d}x^2 } \gt 0$ at $x=a$, we have a minimum.
- If the second derivative is zero: $\dfrac{ \mathrm{d}^2 f }{ \mathrm{d}x^2 }=0$ at $x=a$, we have a point of inflection.

For more detailed information on stationary points, see Stationary Points.
Using the Sign of the First Derivative
Another method used to classify turning points is to look at the sign of the first derivative $\dfrac{\mathrm{d} f}{\mathrm{d} x}$ on either side of the stationary point. If:
- The first derivative is positive on the left hand side of the turning point and negative on the right hand side, we have a maximum.
- The first derivative is negative on the left hand side of the turning point and positive on the right hand side, we have a minimum.
- In any other case, the stationary point is a point of inflection.
Points of Inflection
Points of inflection are stationary points where the graph of a function changes from being |concave to |convex (a rising point of inflection), or convex to concave (a falling point of inflection).
At a point of inflection, the slope of the function is neither increasing nor decreasing. Consequently, the second derivative of the function will be equal to zero. Once we have found a stationary point of a function, we can therefore determine whether the point is a point of inflection by finding the second derivative of the function. If it is equal to zero, then we have found a point of inflection.
But how do we know whether we have a rising or falling point of inflection? The answer is to take the third derivative $\dfrac{\mathrm{d}^3 f}{\mathrm{d} x^3}$ of the function:
- If the third derivative is positive $\left(\dfrac{\mathrm{d}^3 f}{\mathrm{d} x^3}\gt 0\right)$, we have found a rising point of inflection (an upward-flowing curve). For example, the graph of $y=x^3$ has a rising point of inflection at $x=0$ since the graph changes from being concave to convex.

- If the third derivative is negative $\left(\dfrac{\mathrm{d}^3 f}{\mathrm{d} x^3}\lt 0\right)$, we have found a falling point of inflection (a downward-flowing curve). For example, the graph of $y=-x^3$ has a falling point of inflection at $x=0$ since the graph changes from being convex to concave.

- If the third derivative is zero, we do not have a point of inflection.
Global versus Local Maxima and Minima
A maximum value of a function is a global maximum if it is the highest output value that a function ever reaches over its entire domain. Similarly, a global minimum is the lowest output value a function ever reaches over its entire domain. Any maximum or minimum that isn't global is called local.
A local maximum is the maximum value that the output of a function reaches across partof the domain. Similarly for a local minimum.
Once we have found the turning point(s) of a function, we can determine whether we have found a local maximum (or minimum) or a global maximum (or minimum) by looking at the shape of the graph of the function (see the example below).
Note: There can only be one global maximum (and/or one global minimum) but there can be more than one local maximum or minimum.
Worked Example
Find any turning points of the function $y=x^3-10x^2+25x+4$ and specify whether each turning point is a global maximum or minimum, or a local maximum or minimum.
Solution
Since all turning points are stationary points, we can use the method for finding stationary points to find the turning points of this function:
1) The first derivative of the function $y=x^3-10x^2+25x+4$ with respect to $x$ is: \[\dfrac{\mathrm{d} y}{\mathrm{d} x}=3x^2-20x+25\]
2) Setting this equal to zero gives: \[3x^2-20x+25=0\]
3) We must now solve the above equation for $x$. Using the quadratic formula with $a=3$, $b=-20$ and $c=25$ gives $x=5$ or $x=\frac{5}{3}$. There is a stationary point at $x=5$ and $x=\frac{5}{3}$. The corresponding $y$ values at each of these points are found by substituting each value of $x$ into the function:
- For $x=5$, we have
\begin{align} y&=5^3-10\times 5^2+25\times 5+4\\ &=125-250+125+4\\ &=4 \end{align}
- For $x=\dfrac{5}{3}$, we have
\begin{align} y&=\left(\frac{5}{3}\right)^3-10\times \left(\frac{5}{3}\right)^2+25\times \frac{5}{3}+4\\ &=\frac{608}{27} \end{align} So the stationary points of the function $y=x^3-10x^2+25x+4$ are at and $(5,4)$ and $\left(\dfrac{5}{3},\dfrac{608}{27}\right)$.
4) For this example we will use the second derivative test to determine whether each of these stationary points is a maximum, a minimum, or a point of inflection.
We find the second derivative of the function $y=x^3-10x^2+25x+4$ by differentiating the first derivative, $\dfrac{\mathrm{d} y}{\mathrm{d} x}=3x^2-20x+25$, with respect to $x$: \[\dfrac{\mathrm{d}^2 y}{\mathrm{d} x^2}=6x-20\] We must now look at the sign of the second derivative at each of the stationary points that we have found. When:
- $x=\frac{5}{3}$ the second derivative is:
\begin{align} \dfrac{\mathrm{d}^2 y}{\mathrm{d} x^2}&=6x-20\\ &=6\times \frac{5}{3}-20\\ &=-10 \end{align} Since $(-10)$ is less than zero, the second derivative is negative at this stationary point and so we have found a maximum.
- $x=5$ the second derivative is:
\begin{align} \dfrac{\mathrm{d}^2 y}{\mathrm{d} x^2}&=6x-20\\ &=6\times 5-20\\ &=10 \end{align} Since $10$ is greater than zero, the second derivative is positive at this stationary point and so we have found a minimum.
Now, the original function, $y=x^3-10x^2+25x+4$, is a cubic function. All cubic functions have the shape of an “S” tilted on its side. When:
- The coefficient in front of the $x^3$ term is positive, as $x$ tends towards positive infinity (becomes larger and larger), $y$ also tends towards positive infinity, while as $x$ tends towards minus infinity (becomes more and more negative), $y$ also tends towards minus infinity, so the graph will look like this:
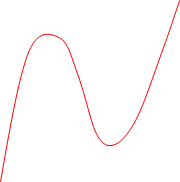
- The coefficient in front of the $x^3$ term is negative, as $x$ tends towards positive infinity (becomes larger and larger), $y$ tends towards negative infinity, while as $x$ tends towards minus infinity, $y$ tends towards positive infinity, so the graph will look like this:

In either case, we can see that any turning points of a cubic function can only be local maxima or minima. The global maximum and minimum of a cubic function do not exist.
The maximum and minimum points of the function $y=x^3-10x^2+25x+4$ found above are therefore the local maximum and minimum points of the function.
Economic Applications
The worked examples below demonstrate how the above methods for optimisation can be used in economics.
Worked Example 1
Suppose that a company which enjoys monopoly power in the calculator market wants to know how many calculators it should produce to maximise its profit. The company’s daily profit (in $£$), is given by $\pi (q)=100q-0.1q^2$ where $q$ is the quantity of calculators sold per day. How many calculators should the company sell to maximise profit and what is the maximum daily profit?
Solution
To determine the quantity $q$ of calculators which maximises profit we must first find the derivative of the profit function $\pi (q)=100q-0.1q^2$:
\[\pi '(q)=100-0.2q\]
We must then set this derivative equal to zero and solve for $q$ as follows: \begin{align} 100-0.2&q=0\\ \Rightarrow 0.2&q=100\\ \Rightarrow &q=500 \end{align}
So the function $\pi (q)=100q-0.1q^2$ has a turning point when $q=500$, but is this a maximum? To answer this question we will use the second derivative test. To find the second derivative of the function we must differentiate the first derivative. This gives: \[\pi ''(q)=-0.2\]
As the second derivative does not depend on $q$ (it is a constant), it will be equal to $-0.2$ (negative) for all values of $q$. As $-0.2$ is negative, we have found a maximum and so the company should sell $500$ calculators per day to maximise profit. Another way to see that $q=500$ is a maximum is to plot the function $\pi (q)=100q-0.1q^2$:

We can see from the graph that the function $\pi (q)=100q-0.1q^2$ takes the highest value when $q=500$ and that the slope changes from being positive when $q\lt500$ to negative when $q\gt500$.
We now wish to find the maximum daily profit for the company. To do this we substitute the profit-maximising quantity of calculators sold, $q=500$, into the profit equation $\pi (q)=100q-0.1q^2$:
\begin{align} \pi (5)&=100×500-0.1×(500)^2\\ &=50,000-25,000\\ &=25,000\\ \end{align}
so the company’s maximum daily profit is $£25,000$.
Worked Example 2
Suppose that a bakery's total cost function is given by: \[TC(q)=5q^2-40q+125\] where $q$ is the number of break loaves produced by the bakery.
a) Write expressions for the bakery's fixed and variable costs. For what value of $q$ are the firm's variable costs minimized?
b) Find the marginal cost and average cost functions.
c) Show that MC$=$AC when AC is at its minimum.
Solution
a) A firm's total costs are made up of its fixed and its variable costs. Fixed costs are constant (do not depend on the quantity of output produced) while variable costs vary with output. The constant term in the bakery's total cost function is $125$ so the bakery's fixed costs are $125$. The bakery's variable costs must therefore be given by: \[5q^2-40q+125-125=5q^2-40q\].
To find the value of $q$ which minimises the firm's variable costs, we must first differentiate $5q^2-40q$ with respect to $q$. This gives $10q-40$. We then need to set this derivative equal to zero and solve for $q$: \begin{align} 10q-40&=0\\ \Rightarrow 10q&=40\\ \Rightarrow q&=4 \end{align}
So the firm's variable costs are minimised when the firm produces $4$ loaves of bread.
b) We can obtain a firm's marginal cost (MC) function by differentiating the total cost function with respect to $q$. For the given total cost function, this gives: \begin{align} MC(q)&=TC'(q)\\ &=10q-40 \end{align}
Notice that this is the same as the derivative of the variable cost function. This makes sense as the derivative of a constant (fixed costs) is zero.
A firm's average cost (AC) is defined as total cost divided by output. Dividing the bakery's total cost function by $q$ gives: \begin{align} AC(q)&=\dfrac{TC(q)}{q}\\ &=\dfrac{5q^2-40q+125}{q}\\ &=5q-40+\dfrac{125}{q} \end{align}
c) To find the value of $q$ which minimises the bakery's average cost, we must first differentiate the bakery's average cost function. This gives: \[AC'(q)=5-\dfrac{125}{q^2}\] We must then set this derivative equal to zero and solve for $q$: \begin{align} 5-&\dfrac{400}{q^2}=0\\ &\Rightarrow 5=\dfrac{125}{q^2}\\ &\Rightarrow q^2=\dfrac{125}{5}\\ &\Rightarrow q^2=25\\ &\Rightarrow q=5\text{ (since }q\text{ cannot be negative)}\\ \end{align} So the bakery's average costs are minimised when $q=5$. Now, when $q=5$ the firm's marginal cost is: \begin{align} MC(5)&=10\times 5-40\\ &=10 \end{align} and the firm's average cost is: \begin{align} AC(5)&=5\times 5-40+\dfrac{125}{5}\\ &=25-40+25\\ &=10 \end{align} So when $q=5$ both the bakery's average cost and its marginal cost are both equal to $10$.
Worked Example 3
Suppose that the inverse demand function for lawnmowers is $p=-\dfrac{1}{4}q+300$. a) Find the total revenue function and the marginal revenue function.
b) Find the price and quantity of lawnmowers which maximise total revenue.
Solution
a) Total revenue is equal to the price of the good multiplied by the quantity sold. Since the subject of the inverse demand function is the market price $p$, we can obtain the total revenue function from the inverse demand function by multiplying the inverse demand function by $q$. This gives: \begin{align} TR(q)&=q\left (-\dfrac{1}{4}q+300\right )\\ &=300q-\dfrac{1}{4}q^2 \end{align}
We can then obtain the marginal revenue function by differentiating the total revenue function with respect to $q$: \begin{align} MR(q)&=TR'(q)\\ &=300-2\times \dfrac{1}{4}q\\ &=300-\dfrac{1}{2}q \end{align}
b) To determine the quantity of lawnmowers which maximises total revenue, we must differentiate the total revenue function, set the derivative equal to zero and solve for $q$: \begin{align} TR'(q)&=300-\dfrac{1}{2}q\;\;\;\text{ (from part}\textbf{ a)}\text{)}\\ \Rightarrow 300&-\dfrac{1}{2}q=0\\ \Rightarrow q&=2\times 300\\ \Rightarrow q&=600 \end{align} So the revenue-maximising quantity of lawnmowers is $600$. From the inverse demand function, when $q=600$ we know that \begin{align} p&=-\dfrac{1}{4}\times 600+300\\ &=-150+300\\ &=150 \end{align} So the revenue-maximising price per lawnmower is $150$.
Test Yourself
Test yourself: Numbas test on differentiation
Test yourself: Numbas test on differentiation, including the chain, product and quotient rules
External Resources
- Differentiation by Maths Tutor
- Introduction to differentiation and differentiation by first principles by Maths is Fun
- Derivative Rules by Maths is Fun
- Differentiation from first principles by mathcentre
- Basic differentiation - a refresher workbook by mathcentre.
- Table of derivatives leaflet by mathcentre.
- Taking derivatives at Khan Academy